0

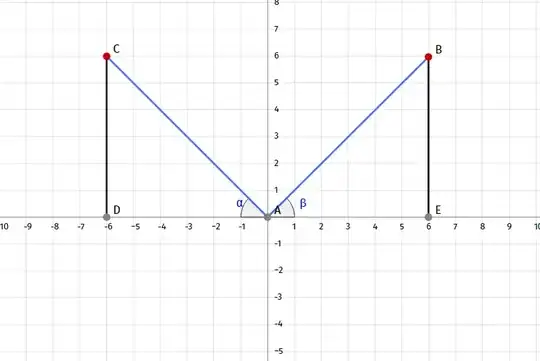
I will make use of a diagram to ask the question I am asking. First of all, consider this diagram:

enter image description here

This will be enough for me to ask a question.

Now, let $AC=AB=1$, which means both hypotenuse are radius of a unit circle.

Trigonometric functions for $\beta$ are defined as:
$\sin\beta=\dfrac{BE}{AB}$ , $\cos\beta=\dfrac{AE}{AB}$ and $\tan\beta=\dfrac{BE}{AE}$

This definition of trig functions is very intuitive and self-explanatory. Now, the problem here is that this definition holds only for $\beta\in \left[ 0 , \dfrac{\pi}{2} \right]$.

The definition for obtuse or reflex angles is based the quadrant in which the terminal side of the angle lies in. For instance, lets say we want to define the functions for $\angle CAE$. Since $CA$ lies in the second quadrant, following are the definitions:

$\sin CAE=\dfrac{CD}{AC}$ , $\cos CAE=\dfrac{AD}{AC}$ and $\tan CAE=\dfrac{CD}{AD}$

Now, I haven't seen any proof of why the trig functions of $\angle CAE$ will be equal to the trig functions of an acute angle, with some sign differences, as in this case, trig functions of $\angle CAE$ are equal to those of $\alpha$, with $cos$ and $tan$ functions negative. Is there any proof to it, or is this an intuitive thing that I am not able to grasp?

Another thought that came to my mind was that these functions are just relationships between the sides of a triangle. But, can a side be negative, so can geometry be applied to negative axes too?

mvw
  • 34,562
codetalker
  • 2,419

1 Answers1

1

You're almost there. The definitions of the trig functions you give are based on ratios in right triangles. Therefore, they are only defined for acute angles (since the sum of angles in a triangle is 180º, and one angle is 90º, the other 2 angles must be acute).

For angles greater than 90º, we use the unit circle, a circle with center at the origin and radius of 1 unit. We insert a right triangle with hypotenuse = 1 into the unit circle (the hypotenuse coinciding with the radius) and apply the ratio definitions of sine and cosine. unit circle

The image shows an angle of 30º, but the principle applies to all angles. And the principle is this: Consider the point where the hypotenuse intersects the circle. The $x$-coordinate of this point is equal to the length of the adjacent leg of the triangle. The $y$-coordinate of this point is equal to the length of the opposite leg. So on the unit circle, we define sine as the $y$-coordinate of the point on the unit circle subtended by the angle. Likewise, cosine is the $x$-coordinate.

[The graphic above, borrowed from the web, is incorrect. The ordered pair (sin, cos) should read (cos, sin).]

Now we can extend the definitions of sine and cosine to all quadrants. In the second quadrant, for angles between 90º and 180º, you can see all $x$-coordinates are negative, but all $y$-coordinates are positive. That is why cosine is negative in the 2nd quadrant, but sine remains positive.

Since tangent is simply $\frac{sin}{cos}$, if one of cosine or sine is negative, then tangent is too. If they are both negative, then tangent will be positive.

scott
  • 1,607
  • I agree with you, but can you solve this problem for me: Suppose there is an obtuse triangle. Now, we drop a perpendicular lying outside the triangle, and extend the base. Now, cosine of the obtuse angle will be equal to the cosine of the linear pair angle adjacent to it, which will be negative, which means that the base of the right triangle formed will be negative. Is this true? – codetalker Jun 23 '16 at 15:40
  • @Siddhant Absolutely true. Base of the right angled triangle is on the negative side of the origin (negative $X$ axis). – Qwerty Jun 23 '16 at 15:44
  • But, @Qwerty, can a length be negative? – codetalker Jun 23 '16 at 15:48
  • @Siddhant In trigonometry you consider displacements not distances.. Mathematics with angle becomes easy when every thing is measured from the angle you are concerned with. That's the reason every proof of trigonometry puts the concerned angle at the origin – Qwerty Jun 23 '16 at 16:03
  • @Qwerty, thnx a lot – codetalker Jun 23 '16 at 16:07
  • @Siddhant, Qwerty is absolutely correct. But I would also remind you that cosine is a ratio, not a length. – scott Jun 23 '16 at 16:10
  • @codetalker - Yes. There is such a thing as directed length, but, honestly, I find it confusing. Just use the triangles as "referece" triangles and use the $(x,y)$-coordinates instead of adjacent and opposite. It really amounts to the same thing. – Steven Alexis Gregory Mar 22 '18 at 03:14