How to rotate a 3D vector on the surface of a plane by a known angle?

Question

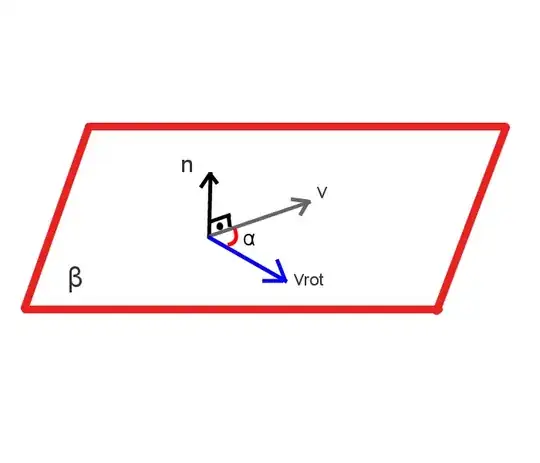
Available data

1. The plane β which is defined by a normal vector n and point P.
2. The vector v which lies on the surface of the plane.(the angle between v and n is 90 degrees).
3. The angle α to which v should be rotated.

---

How to obtain the rotated vector(vrot) ?

Note that the vectors are 3D.

Answer 1

If $v \neq 0$ and $n$ is a unit vector, the vectors $v$ and $n \times v$ are an orthogonal basis of your plane, and the result of rotating $v$ counterclockwise (about $n$) by an angle $\alpha$ is $$ (\cos\alpha)\, v + (\sin\alpha)\, (n \times v). $$