4

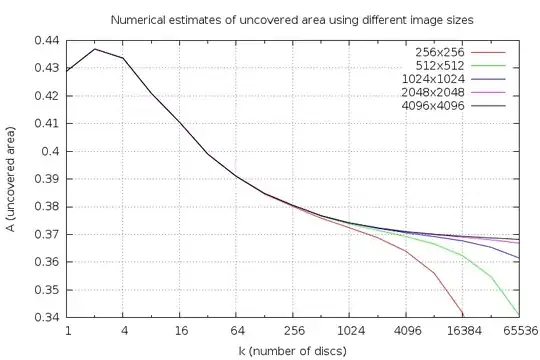
1. Paint a $1\times 1$ square in blue.

2. Take $k$ points randomly and uniformly from the square.

3. Paint $k$ disks of area $1/k$ centered at each point in red.

What is the expected remaining blue area?

Remark: the sum of the areas of the disks is $k\cdot 1/k=1$, the same as the area of the square, but we have to account for:

  1. Disks intersecting each other.
  2. Disks intersecting the outside of the square.
Community
  • 1
nmamg
  • 139
  • 6

2 Answers2

5

A naive approach that will be close for large $k$ is to say a point has $\frac {k-1}k$ chance of not being covered by a given disk, so $\left(\frac{k-1}k\right)^k$ chance of not being covered at all. The limit in large $k$ is that $\frac 1e$ is not covered. This is not quite right as points near the edge have lower chance of being covered. The corner points can only be covered if the center of the disk is in an area $\frac 1{4k}$ so the chance of coverage by one disk is $\frac {4k-1}{4k}$. Raising that to the $k$ power has limit $e^{-1/4}\approx 0.7788$ of not being covered. The side points have a chance of $e^{-1/2}$, but the area of reduced probability of coverage gets small as $k$ gets large.

Ross Millikan
  • 374,822
2

Here is some C code using OpenGL to estimate numerically. And a plot of the results (I plotted different image sizes to get a sense of how well it approximates the true value). The limit seems to agree with Ross's analytic answer.

numerical estimates

Claude
  • 5,647
  • It should be true that the uncovered area approaches $\frac 1e$ from above. The area that has greater probability to not be covered is a strip of width $\frac 2k$ around the edge of the square. This strip gets smaller as $k$ gets larger. – Ross Millikan Jun 20 '16 at 03:04
  • @Ross: I think you're right, but you'd also need to argue that this error dominates the one from replacing $\left(1-\frac1k\right)^k$ by $\mathrm e^{-1}$, which has the other sign. – joriki Jun 20 '16 at 10:50