In the course of writing a(n Honours) thesis, I'm searching for a proof to a conjecture that appears very likely to be true. Many results will rely upon it. My own attempts to prove it have been unfruitful, and at this point I'd be happy to settle for a reference to something in the literature.
Here's the conjecture:
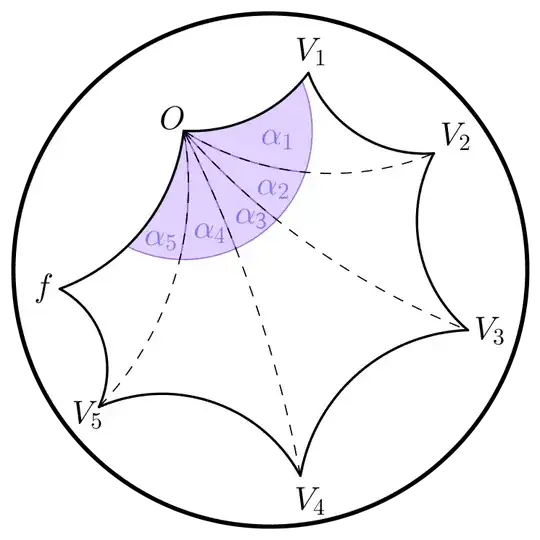
Let $O,V_1, \dots V_{n-2} ,f$ be an $n-$pointed convex polygon in $H^2$. Given all outer angles (those between adjacent edges of the polygon), and angles $\angle V_n O V_m$ and $\angle V_{n-2} O f$, the entire polygon is uniquely determined up to isometry.
Pictorial statement of the conjecture:
Given all outer angles of an $n-$pointed convex polygon, and all $\alpha_i$, the full geometry of the shape is determined up to isometry.