Evaluate $\int_0^{\infty} \frac{\log(x)dx}{x^2+a^2}$ using contour integration

Question

This question is Exercise 10 of Chapter 3 of Stein and Shakarchi's Complex Analysis.

Show that if $a>0$, then

$$\int_0^{\infty} \frac{\log(x)dx}{x^2+a^2}=\frac{\pi \log(a)}{2a}.$$

The hint is to integrate over the boundary of the domain $\{z: \epsilon<|z|<R, \Im(z)>0\}.$

I'm not sure what to do with the integral over the outer arc.

Answer 1

Take these lines as a long comment and not an answer, but the integral is trivial to compute through real-analytic techniques. For any $a>0$ we have:

$$ \int_{0}^{+\infty}\frac{\log(x/a)}{a^2+x^2}\,dx = \frac{1}{a}\int_{0}^{+\infty}\frac{\log x}{1+x^2}=\color{red}{0} $$ since the substitution $x\mapsto\frac{1}{x}$ gives $\int_{1}^{+\infty}\frac{\log x}{1+x^2}\,dx = -\int_{0}^{1}\frac{\log x}{1+x^2}\,dx $.
On the other hand, $$ \int_{0}^{+\infty}\frac{\log(a)}{a^2+x^2}\,dx = \frac{\log a}{a}\int_{0}^{+\infty}\frac{dx}{1+x^2}=\color{red}{\frac{\pi\log a}{2a}}.$$

If you want to use contour integration, you may take a semicircular contour in the right half-plane with three bulges around $z=0$ (singularity for $\log z$) and $z=\pm i a$ (singularities for $\frac{1}{z^2+a^2}$), then apply the residue theorem. The integral over the outer arc is vanishing as $R\to +\infty$ since it is bounded by $\frac{2\pi\log R}{R}$ in absolute value for any $R$ big enough.

Answer 2

If you stick to the complex-analytic technique, here is one possible solution: Choose the branch cut of complex logarithm as $[0, \infty)$ so that $\Im\log z \in [0, 2\pi)$. Then consider the function

$$ f(z) = \frac{\log^2 z}{z^2 + a^2}, $$

where $\log^2 z = (\log z)^2$ is the square of the logarithm. Then using the keyhole contour $C$ described as in Figure 1,

$\hskip{2in}$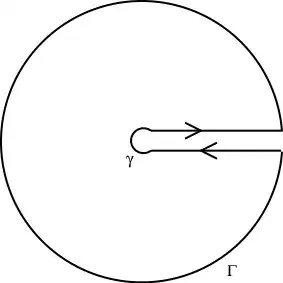

$\hskip{1in}$ Figure 1. Image from @Daniel Fischer♦'s answer in this posting.

we find that

\begin{align*} \oint_{C} f(z) \, \mathrm{d}z &= 2\pi i \left( \underset{z=ia}{\operatorname{Res}} f(z) + \underset{z=-ia}{\operatorname{Res}} f(z) \right) \\ &= \frac{\pi}{a} \left( \left(\log a + \frac{i\pi}{2} \right)^2 - \left(\log a + \frac{3i\pi}{2} \right)^2 \right) \\ &= \frac{2\pi^3}{a} - \frac{2\pi^2 i \log a}{a}. \tag{1} \end{align*}

On the other hand, shrinking the inner circle $\gamma$ to the origin and letting the outer circle $\Gamma$ to the infinity, it follows that

$$ \oint_{C} f(z) \, \mathrm{d}z \xrightarrow[\substack{\gamma \to 0 \\ \Gamma \to \infty}]{} \int_{0}^{\infty} \frac{\log^2 x}{x^2 + a^2} \, \mathrm{d}x - \int_{0}^{\infty} \frac{(\log x + 2\pi i)^2}{x^2 + a^2} \, \mathrm{d}x. \tag{2} $$

Comparing imaginary parts of $\text{(1)}$ and $\text{(2)}$, it follows that

$$ \int_{0}^{\infty} \frac{\log x}{x^2 + a^2} \, \mathrm{d}x = \frac{\pi \log a}{2a}. $$

Answer 3

Notice that the real part of $f (z)= \frac {\log (z)}{z^2+a^2}$ is symmetric along the origin. Then $$Re \int_{-R}^{R}f (z)dz=2\int_{0}^{R}f (x)dx$$ Now we close the contour by making a semicircle of radius $R $ along the positive imaginary axis and take the limit as $R \to \infty $. So $$\int_{\gamma}\frac {\log(z)}{z^2+a^2}dz=\int_{-R}^{R} \frac {\log(x)}{x^2+a^2}dx+\int_{\gamma'}\frac { \log(z)}{z^2+a^2}dz$$ Where $\gamma'$ is the top part of the semicircle. By the Estimation Lemma the top integral is bounded as $$\left|\int_{\gamma'}\frac {\log(z)}{z^2+a^2}dz \right| \le \pi\frac { \sqrt {(\log^2(R)+\pi^2)}}{R} $$ which vanishes as $R \to \infty $. Now since the value of the real integral is the only contribution to the contour integral we apply the Residue Theorem $$\int_{-\infty}^{\infty} \frac {\log(x)}{x^2+a^2}dx= \pi \frac {\log(a)+i\pi/2}{a}$$ But since we are not integrating over the branch cut in $$\int_{0}^{\infty} \frac {\log (x)}{x^2+a^2}dx$$ and the real part is symmetric we can conclude $$\int_{0}^{\infty} \frac { \log(x)}{x^2+a^2}dx=\pi \frac { \log(a)}{2a}$$

Answer 4

Since the OP requests evaluation by contour integration, we proceed accordingly.

We begin by analyzing the contour integral $I$ as given by

$$I=\oint_C \frac{\log^2(z)}{z^2+a^2}\,dz$$

where $C$ is the classical "keyhole" contour with the "keyhole" aligned with the branch cut taken along the non-negative real axis.

Then, we have using the residue theorem

$$\begin{align} I&=2\pi i \left(\frac{(\log(a)+i\pi/2)^2}{2ia}+\frac{(\log(a)+i3\pi/2)^2}{-2ia}\right)\\\\ &=-i 2\pi^2 \frac{\log(a)}{a}+\frac{2\pi^3}{a} \tag 1 \end{align}$$

We also have

$$\begin{align} I&=\int_0^\infty \frac{\log^2(x)}{x^2+a^2}\,dx+\int_\infty^0 \frac{(\log(x)+i2\pi)^2}{x^2+a^2}\,dx\\\\ &=i4\pi \int_0^\infty \frac{\log(x)}{x^2+a^2}\,dx+4\pi^2 \int_0^\infty \frac{1}{x^2+a^2}\,dx\\\\ &=-i4\pi \int_0^\infty \frac{\log(x)}{x^2+a^2}\,dx+ \frac{2\pi^3 }{a} \tag 2 \end{align}$$

Now, set real and imaginary parts of $(2)$ and $(3)$ equal to arrive at the result

$$\bbox[5px,border:2px solid #C0A000]{\int_0^\infty \frac{\log(x)}{x^2+a^2}\,dx=\frac{\pi \log(a)}{2a}}$$

Answer 5

The substitution $x=at$ gives:

$$\int_0^{\infty} \frac{\log(x)dx}{x^2+a^2} dx=\frac{1}{a}\int_{0}^{\infty} \frac{\log(at)}{1+t^2} dt$$

$$=\frac{1}{a} \int_{0}^{\infty} \frac{\log t +\log a}{1+t^2} dt$$

Note

$$\int_0^{\infty} \frac{\log(x)dx}{x^2+1}=0$$

This can be proved with the substitution $x=\frac{1}{u}$