- Inside a line segment $E$ with length $6$ unit, there are $2$ segments $A$ with length $2$ unit and $B$ with length $3$ unit.
- The position of $A$ is fixed with its left end being $k$ unit from the left end of $E$. Thus the distance between their right ends will be $\left(\,4 - k\,\right)$ unit,while $B$ can move freely and uniformly inside $E$.
- If a point is chosen randomly on $E$ , find the probability that the point lies inside $A$ and $B$ at the same time.
- 89,464
- 119
-
1This problem is somewhat different from the usual ones, so it would sad if it were closed because you have not mentioned what you have tried. Please do so, by editing the post. – André Nicolas Jun 14 '16 at 03:35
1 Answers
Take left-hand end to have coordinate 0 and right-hand end to have coordinate 6. Let $b$ be the coordinate of the left-hand end of $B$. So $b$ is uniformly distributed on $[0,3]$.
Let the point $X$ have coordinate $x$, so $x$ is uniformly distributed on $[0,6]$.
$X\in B$ iff $x\in[b,b+3]$, and $X\in A$ iff $x\in[k,k+2]$. So for $b\in[-3,k-3]$ we have $A\cap B=\emptyset$. For $b\in[k-3,k-1]$ we have $A\cap B=[k,b+3]$. For $b\in[k-1,k]$ we have $A\cap B=A$. For $b\in[k,k+2]$ we have $A\cap B=[b,k+2]$ and for $b\in[k+2,6]$ we have $A\cap B=\emptyset$.
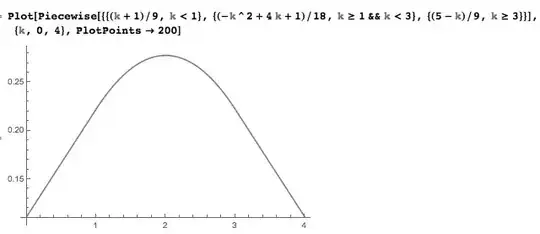
Case 1: $k<1$. $18p(x\in A\cap B)=\int_0^k2\ db+\int_k^{k+2}(k+2-b)\ db=2(k+1)$.
Case 2: $1\le k<3$. $18p(x\in A\cap B)=\int_0^{k-1}(b+3-k)db+\int_{k-1}^k2\ db+\int_k^3(k+2-b)db=-k^2+4k+1$
Case 3: $3<k\le4$. $18p(x\in A\cap B)=\int_{k-3}^{k-1}(b+3-k)db+\int_{k-1}^32\ db=2+8-2k=10-2k$
$\textbf{Comment}$
Piecewise functions are fiddly and it is easy to make mistakes. So one needs to do some basic checking. (1) Is the result continuous? (Answer: yes), (2) Does the graph look plausible (no obvious odd wiggles etc) (Answer: yes), (3) Does it respect any obvious symmetries in the problem? (The obvious symmetry here is that the probability should be the same for $k=2\pm h$, which it is.)
- 18,380
-
Thanks again . But , sorry ! May be I have not mentioned clear enough . For the statement " B can move freely and uniformly inside E ." I have assumed that the whole segment of B must stay inside E (fully) , no part of B can exceed ( outside ) both ends of E . I apologize for my carelessness ! – mrwong Jun 15 '16 at 10:30
-
Does your graph show that when k = 0 then P will be about 1/9 = 0.11 and when k = 2 then P will be at its maximum value of about 0.28 ? What will be the average value of P ? What will be the values of k for a P of 0.25 ? – mrwong Jun 19 '16 at 04:40
-
@mrwong Look at the formulae above the graph. Yes, the prob is $\frac{1}{9}$ for $k=0$. Yes, the maximum is at $k=2$ with value $\frac{5}{18}\approx0.27778$. To get the average value of the prob you have to integrate assuming $k$ is equally likely to have any value in $[0,4]$. That gives $\frac{23}{108}\approx 0.2130$. The prob is 0.25 for $k$ satisfying $2k^2-8k+7=0$ which gives $k=2\pm\frac{1}{\sqrt2}\approx$1.2929 or 2.7071. – almagest Jun 19 '16 at 10:00
-
Welcome to join the discussion of this type of problem in www.mathisfunforum.com if you are interested ! – mrwong Jun 20 '16 at 10:25