1

It is a fundamental problem, and there are some related problem asked before:
1. $\epsilon - \delta$ definition to prove that f is a continuous function.
2. How to show that $f(x)=x^2$ is continuous at $x=1$?

However, it seems I am confused about something.
In the definition by the textbook: Advanced Calculus, Folland p.14

The continuity of $f$ on $U$: For every positive number $\epsilon$ and every $a\in U$, there is a positive $\delta$ so that $$|f(x)-f(a)|<\epsilon \text{ whenever } |x-a|<\delta$$

or there is an equivalent definition:

show that for every $\epsilon >0$ there is $\delta >0$ such that if $0<|x-a|<\delta\,,$ then $|f(x)-f(a)|<\epsilon$.

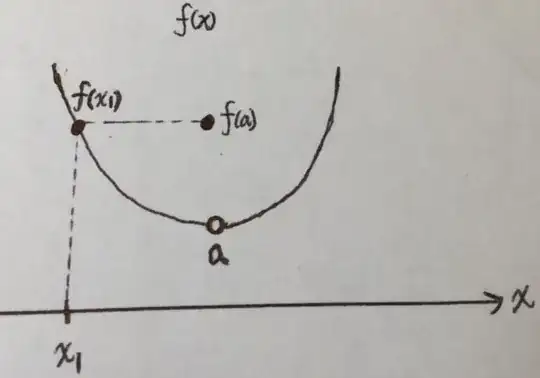
Now, apply this definition in the following picture. Obviously, $f(x)$ is not continuous at $x=a$.
Suppose the distance for the discontinuity gap is $D$.
If I want to use $\delta-\epsilon$ definition to prove this, should I say that:

$|x-a|<\delta$, where $\delta$ is very small; however, $|f(x)-f(a)|\rightarrow D$ at least. So it is not for all $\epsilon$.

Or should I say that:

$|f(x)-f(a)|\leq \epsilon$ where $\epsilon$ is very small; however, $|x-a|$ is about $|x_1-a|$ by the symmetry of the second order curve; which cannot be smaller anymore.

My question is:

Let $\epsilon = 0.00001 << D$; however, I can still find $x$ around $x_1$ such that there indeed exists $\delta = |x_1-a|$ such that $|f(x)-f(a)|\leq \epsilon$. So how do I define "small"? Which part I made mistakes?

enter image description here

Community
  • 1
sleeve chen
  • 8,281
  • Yes, I want a conceptual answer, not coming up with a trick to find $\delta$ like the answer in the reference link. That is why I do not say what the function really is. – sleeve chen Jun 13 '16 at 21:21
  • 3
    I think you might be having trouble negating the quantifiers. What you need to show is that there is an $\epsilon > 0$ such that for any $\delta > 0$, there is an $x$ with $|x-a|<\delta$ and yet $|f(x)-f(a)|>\epsilon$. – Callus - Reinstate Monica Jun 13 '16 at 21:25

1 Answers1

1

In general, you want to find an $\epsilon$ such that it is impossible to find a $\delta$ such that for all $x$ within a distance of less than $\delta$ of $a$, $f(x)$ is within a distance of less than $\epsilon$ of $f(a)$. Note that if $\epsilon$ is smaller than $D$, than no matter how close $x$ gets to $a$, $f(x)$ will be farther than $\epsilon$ from $f(a)$.

For your last question: your mistake is that you found only a single value of $x$ such that $|x-a|< \delta$ and $|f(x)-f(a)| < \epsilon$. It needs to hold for all $x$ with $|x-a|<\delta$. To see that this is not the case, consider the point $x_2 = (x_1 + a)/2$. Then $|x_2-a| < \delta$, but $|f(x_2)-f(a)|$ is larger than $\epsilon$.

Jakob Hansen
  • 1,387