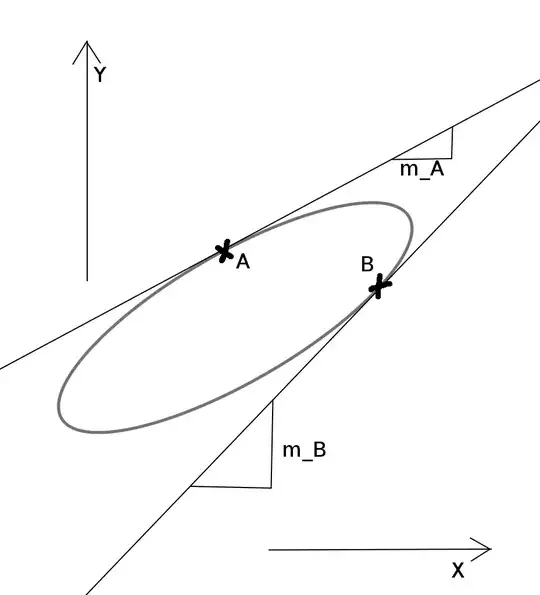
I have encountered a rather complex issue that I could not solve on my own, and my research online has so far not yielded a suitable answer to my question, hence my decision to seek help in this place. I generally want to fit an ellipse to two points in a two-dimensional space whose tangents are known. Here is a more detailed explanation:
What I have: I have information on the position of two points only relative to each other (point A and point B) in a two-dimensional space, and the slope of the tangents through these points (m_A and m_B). This means the orientation of these points in the cartesian coordinate system is known, their exact coordinates relative to the origin however are not, as an origin is not (yet) defined.
What I seek: The general solution for a tilted, off-centered ellipse in 2-D space. Most formulas for tilted ellipses I found so far assume it to be centered, which does unfortunately not work for me, as I only know the relative coordinates of my points to each other and hence cannot solve it under the assumption that their exact position is known (this would require a given origin at a known ellipse center; I assume setting one of my points as the origin and taking the ellipse as off-centered would avoid this issue).
My questions:
1) Can I assume there is a unique (or finite number of) solution(s) for this problem?
2) If yes, (and if you have the time) can you help me find the general solution for this issue?
The image below might help to illustrate my problem.