I'm trying to find an indexed family {An:n∈N} that satisfies:
- each An is an infinite subset of the naturals N
- the intersection of any two arbitrary sets is empty
- the union of all the subsets is is the naturals N
I'm trying to find an indexed family {An:n∈N} that satisfies:
Let $f\colon \Bbb N \times \Bbb N \to \Bbb N$ be any bijection, for example $$ f(a,b) = \frac {(a+b)(a+b+1)} 2 + b. $$ Define $$ A_n = \{f(n, k) \mid k \in \Bbb N\}, \quad \text{for $n\in\Bbb N$}. $$ Then the $A_n$ are pairwise disjoint and their union is $\Bbb N$. Every $A_n$ is infinite, because for each $n$, $k \mapsto f(n,k)\colon \Bbb N \to \Bbb N$ is an injection.
Given any ordering the natural numbers, just assign every number to an entry of an infinite matrix following the same diagonal path as in the proof that the rational numbers are countable. 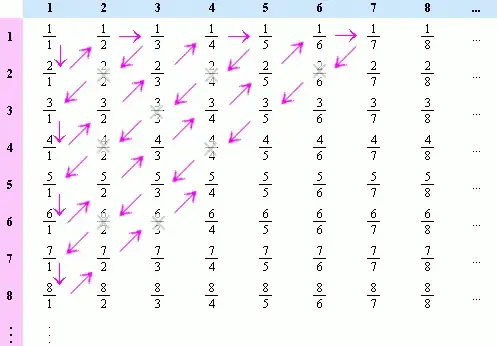 .
.
Define $A_n$ to be the set of all natural numbers on the $n$-th row. Needless to say that each $A_n$ is infinite.
There are as many ways of performing this task as there are orderings of $\mathbb{N}$.