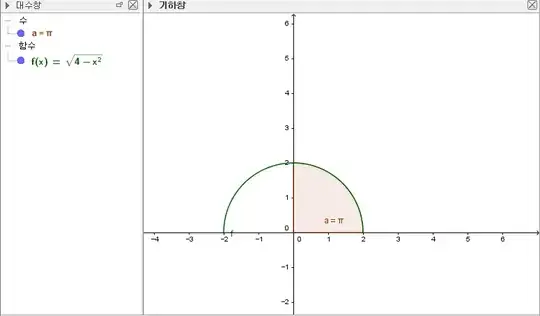
I'm trying to figure out how to go about this, but I'm not entirely sure. Is there a specific way to find the area under a curve or line (and strictly above the x-axis) before doing Riemann sums?
Asked
Active
Viewed 118 times
2 Answers
1
It is quarter of the circle whose radius is $2$ and center origin, so the answer is $\pi$.
You can also substitute $x=2\sin \theta\;(0 \le \theta \le \frac{\pi}{2})$, then \begin{align} \int_0^2 \sqrt{4-x^2}dx &= \int_0^{\frac{\pi}{2}} 2\cos \theta\sqrt{4-4\sin^2\theta} d\theta\\ &=\int_0^{\frac{\pi}{2}} 4\cos^2\theta d\theta\\ &=\int_0^{\frac{\pi}{2}} 4 \frac{1+\cos 2\theta}{2}d\theta\\ &=\left[2\left(\theta+\frac{1}{2}\sin2\theta\right)\right]_0^{\frac{\pi}{2}}\\ &=\pi \end{align}
choco_addicted
- 8,786
- 8
- 24
- 53
-
That sort of makes sense, but is there any algebra to show that? – user10984587 Jun 08 '16 at 12:56
-
@user10984587 I'll edit my post to show it. Wait a minute, please :) – choco_addicted Jun 08 '16 at 12:57
-
I'll take a stab and say you use the integral and the integral of $\sqrt{4-x^2}$ at $x=2$ is pi + constant? – user10984587 Jun 08 '16 at 13:00
-
@user10984587 I can't understand what "the integral of $\sqrt{4-x^2}$ at $x=2$" is. – choco_addicted Jun 08 '16 at 13:04
-
I meant what you just showed. Thanks for the explanation! – user10984587 Jun 08 '16 at 13:09
1
substitute $$x=2\sin { \theta } \\ dx=2\cos { \theta d\theta } $$ and change bounders so that: $$\int _{ 0 }^{ 2 }{ \sqrt { 4-{ x }^{ 2 } } dx } =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \sqrt { 4-4\sin ^{ 2 }{ \theta } } } 2\cos { \theta d\theta } =4\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \cos ^{ 2 }{ \theta } d\theta = } 2\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \left( 1+\cos { 2\theta } \right) d\theta = } 2{ \left( \theta +\frac { \sin { 2\theta } }{ 2 } \right) }_{ 0 }^{ \frac { \pi }{ 2 } }=\pi \\ \\ $$
haqnatural
- 21,578