Photo image to find the screen orientation

Question

I am trying to find the angle of tilts of a screen using projection of a circle from a source $S$. The light beam falls on the photo screen to expose it and what we get is an ellipse with major axis $a$ and minor axis $b$. The light beam is in the form of a cone so what we get is essentially an ellipse on the screen.

The screen tilts with angle $\alpha$ to the vertical axis $y$ and $\beta$ with the horizontal axis $x$. Rotation about the $z$ axis does not affects the shape of the ellipse so it can be ignored for the moment.

The transformed plane can be given by:

$\begin{bmatrix}x_1\\y_1\\z_1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&\cos\alpha&\sin\alpha\\0&-\sin\alpha&\cos\alpha\end{bmatrix}\cdot\begin{bmatrix}\cos\beta&0&-\sin\beta\\0&1&0\\\sin\beta&0&\cos\beta\end{bmatrix}\cdot\begin{bmatrix}\cos\gamma&-\sin\gamma&0\\\sin\gamma&\cos\gamma&0\\0&0&1\end{bmatrix}\cdot\begin{bmatrix}x\\y\\z\end{bmatrix}$

so ignoring $z$ and setting $\gamma = 0$ we get, $$\ x_1=x\cos\beta \ + \ y\sin\alpha \sin\beta $$ and $$ \ y_1=\ y\cos\alpha$$

Now on the screen $P$ is vertical axis and $Q$ is the horizontal axis, $\theta$ is the angle of semi-major axis with horizontal- $Q$. To get the same ellipse as in the projection we can use the shear transformation of an ellipse on the screen:

Rotation transformation gives:

$$P_1 = P\cos\theta \ - \ Q\sin\theta$$

$$P_2 = P\sin\theta \ + \ Q\cos\theta$$

substituting $P_1$ & $P_2$ in ellipse equation with $a$ & $b$ as major and minor axis followed by vertical shear transformation we can get the limits to the ellipse w.r.t angle $\theta$, which are:

$\sqrt{a^2\sin^2\theta +b^2\cos^2\theta } \ $ for the horizontal axis $Q$

$\sqrt{b^2\sin^2\theta +a^2\cos^2\theta } \ $ for the vertical axis $P$

After being done with that, we do the same procedure using $x_1$ and $y_1$ to apply the transformation to a circle using equation of a circle. After the shear transformation of those equation we get the equations giving the maximum limit:

$\sqrt{a^2\cos^2\alpha +a^2\sin^2\alpha \sin^2\beta } \ $ for horizontal axis

$\sqrt{a^2\cos^2\alpha }\ $ for vertical axis

For getting $\alpha$ and $\beta$ in terms of $\theta$ we use the above equations as the maximum extent of both the cases must be equal to get the same ellipse.

so:

$\sqrt{a^2\cos^2\alpha +a^2\sin^2\alpha \sin^2\beta }=\sqrt{b^2\cos^2\theta +a^2\sin^2\theta }$

and

$\sqrt{a^2\cos^2\alpha }=\sqrt{a^2\cos^2\theta +b^2\sin^2\theta }$

Solving these equation we get:

$$\alpha =\cos^{-1}\sqrt{\cos^2\theta +\frac{b}{a^2}^2\sin^2\theta }$$

$$\beta =\sin^{-1}\sqrt{\frac{\cos^2\theta \left(\frac{b^2}{a^2}-1\right)}{\sin^2\theta \left(1-\frac{b^2}{a^2}\right)-1}}$$

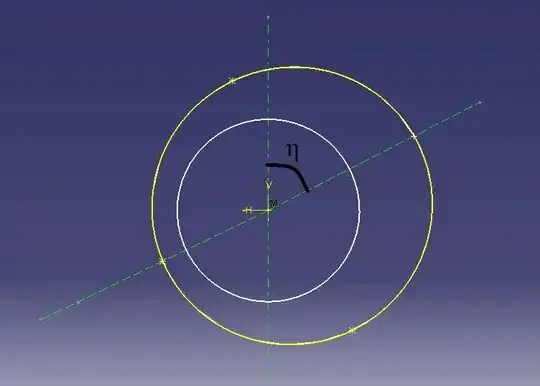
It turns out it is not giving the correct $\alpha$ & $\beta$ values with $\theta$ but when viewed from the point $S$ along the $z$ axis we get the following image in which the small circle is the circle that is being projected and the bigger ellipse(which would appear as a circle) is the projected ellipse on the screen when viewed from point $S$.

Using the angle $\eta$, that is the angle between the vertical axis and the ellipse major axis when viewed from point $S$, in the above angle equations ($\alpha, \beta$) in the place of $\theta$ and keeping the other parameters same, we observe that it gives the correct value of $\alpha$ & $\beta$

Now in general case we cannot use this method ($\eta$) to find the angles as we would just have the screen photo image of the ellipse. Can this $\eta$ be related to $\theta$ by any means or what can be done to change the angles equation to get the correct value?

I am using a software to simulate this so I can see from the source position and get the $\eta$ angle but in practical case it can not be done as we will just have the photo of the ellipse. This is being done to correct the photo(screen) plane using $\alpha$ & $\beta$ so that it can reach the ideal state if being parallel to the plane of the circle.

Answer 1

Okay then. One way to achieve what you want is via the following:

1. First use a combination of $x$ and $y$ rotations to align the $x$ axis with the minor axis of the ellipse.
2. Then rotate about the $x$-axis by angle $\phi$.

(Remark: the following paragraph is new)
To find out the angle $\phi$, we start by thinking about what happens if we wrote a flat screen about its $x$-axis by an angle $\phi$. (An important factor that I forgot to include earlier is the shape of the original cone.) Suppose that the cone you are intersecting comes from the graph $z = \sqrt{\sigma(x^2 + y^2)}$. When $\sigma = 1$ we have a circular cone with a right-angle aperture. A rotation about the $x$-axis by angle $\phi$ results in the ellipse on the screen satisfying the equation $$ \frac{1}{\sigma}(x \sin \phi + c)^2 = \cos^2\phi x^2 + y^2 $$ This gives the ratio of the semi-minor/major axes to be $$ \frac{b^2}{a^2} = \cos^2 \phi - \frac{1}{\sigma} \sin^2\phi $$ (This missing factor of $\sigma$ is why the original result was off by so much.)

From the data provided by the OP in the comments I infer that the number $\sigma$ is somewhere between 90 and 110 in those examples.
(end new stuff)

What we need to do is to rotate the axes to effect step 1. To do so we use the well-known relation that we can get a rotation about the $z$ axes by conjugating a rotation in the $x$ axis with one in the $y$ axis. So step 1 can be attained by

1. First rotating about the $x$ axis by $\pi/2$ radians.
2. Rotating about the $y$ axis by $\theta - \pi/2$ radians (where $\theta$ is the angle from the $x$ axis to the major axis)
3. Rotate about the $x$ axis by $-\pi/2$ radians.

So the final answer is $$ X(\pi/2) Y(\theta - \pi/2) X(\phi - \pi/2) $$

---

Another way is to keep track of where the $z$ axis goes. Since we are looking at intrinsic rotations, what we should do is to first compute the product

$$ X(\alpha) Y(\beta) = \begin{pmatrix} * &* & \sin \beta \\ * & * & - \sin\alpha \cos\beta \\ * & * & \cos\alpha\cos\beta\end{pmatrix} $$

the last column of which represents where the $z$-axis ends up after the transformation. We compare this to

$$ Z(\theta - \pi/2) X(\phi) = \begin{pmatrix} * &* & \sin (\theta - \pi/2) \sin\phi \\ * & * & - \cos(\theta- \pi/2)\sin\phi \\ * & * & \cos\phi\end{pmatrix} $$

where $\theta$ and $\pi$ are as before. Then we can simply solve for $\alpha$ and $\beta$ from the three equalities.

---

You will notice that the first answer requires two rotations about the $x$ axis, while the second only one. The difference is that in the first we insist on lining up the $x$ axis with the minor axis of the ellipse. In the second we don't. The two answers differ by a Z rotation which should be immaterial when you just want to line up the plane of the screen with the light source.

---

More new stuff:

Let's make the assumption that $\sigma = 100$. First consider the data where $\theta = 0$ and $a = 48.722$ and $b = 42.117$ as in this comment. Solving the above equation for $\phi$ we get

$$\cos\phi = \sqrt{ \frac{1 + \frac{\sigma b^2}{a^2}}{\sigma + 1}} = 0.86588\ldots $$

or

$$ \phi \approx 30.0165^\circ$$

and $\theta = 0$ implies $\alpha = 0$ and hence $\beta = \phi$. So far so good.

Next, let's do the case $a = 52.548$, $b = 42.143$, $\theta = 70.269^\circ$ as in this comment. The same expression above gives

$$\cos\phi = \sqrt{ \frac{1 + \frac{\sigma b^2}{a^2}}{\sigma + 1}} = 0.80419\ldots $$

or

$$\phi \approx 36.468^\circ$$

From the above discuss we should have

$$ \sin \beta = \cos\theta \sin \phi = 0.2007\ldots $$

or

$$ \beta \approx 11.58^\circ $$

similarly solving for $\alpha$ we get

$$ \alpha \approx 34.826^\circ $$

These are pretty close to the values of $\beta = 14$ and $\alpha = 34$ given in the set-up of the problem.

(I remark here that with $\alpha = 34$ and $\beta = 14$, and $\sigma = 100$, the predicted values of $a, b, \theta$ are supposed to be

$$ \frac{b^2}{a^2} = 0.64355\ldots $$

[compare with 65.3189... from the given data] and

$$ \theta \approx 65.9693^\circ $$

[compare with 70.269 from the data]. The discrepancy can easily be due to measurement errors, or due to that I only inferred $\sigma$ from the data [disclosure: I don't know how the OP's simulation software works]. But note that uncertainty in $\sigma$ cannot effect the value of $\theta$, only the value of $\phi$.)