8

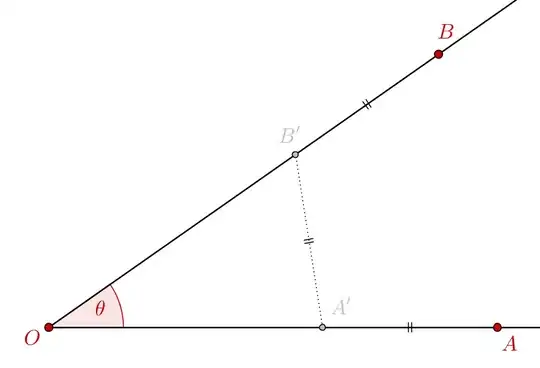
diagram

Three points $A,O,B$ are given, and $0<\theta=\widehat{AOB}<\frac{\pi}{3}$.
It is known that there are two points $A',B'$ on the segments $OA,OB$ such that $$ BB'=B'A'=A'A $$ holds. How to find them with straightedge and compass?

The problem is straightforward to solve through trigonometry: if we set $$OA=A,\;OB=b,\;\cos\theta=c,\; AA'=x$$ it boils down to solving the second-degree equation: $$ (a-x)^2+(b-x)^2 - 2(a-x)(b-x)c = x^2, $$ but I wasn't able to find an elegant solution through straightedge and compass only.

Jack D'Aurizio
  • 353,855
  • Is it possible that the triangles $\Delta AOB,\Delta A'OB'$ are similar? If so, then a simple construction seems immediate. – Semiclassical Jun 03 '16 at 17:41
  • 2
    @Semiclassical: that cannot hold in general. If $AOB$ and $A'OB'$ are similar then $\frac{a-x}{b-x}=\frac{a}{b}$, but we know that $x$ is the solution of an irreducible quadratic equation. – Jack D'Aurizio Jun 03 '16 at 17:43
  • You're right, and it's actually easy to construct a counterexample: If $A'B'$ is perpendicular to $OA$, then there's no way that $AB$ and $A'B'$ can be parallel. – Semiclassical Jun 03 '16 at 17:50

2 Answers2

4

Thanks to Xaver, a simple solution (but a not-so-trivial one).

enter image description here

Lemma 1. If $P\in OA$ and $Q\in OB$ fulfills $PA=QB$, then $PB\cap QA$ lies on a line
that is parallel to the angle bisector of $\widehat{AOB}$.

Lemma 2. $C=AB'\cap A'B$ lies on a fixed circle $\Gamma$ through the incenter of $AOB$,
since $\widehat{ACB}=\frac{\pi+\theta}{2}$.

So, let $P$ be a point of $OA$ and $Q$ be the corresponding $Q$-point on $OB$, as in Lemma 1.

Let $D=BP\cap AQ$ and $\ell$ be the line through $D$ that is parallel to the angle bisector of $\widehat{AOB}$.

Let $I$ be the incenter of $AOB$ and $\Gamma$ the circumcircle of $AIB$.

Then $\color{blue}{C=\ell \cap \Gamma}$ and $A',B'$ are easily found.

Community
  • 1
Jack D'Aurizio
  • 353,855
3

Let $S$ be the intersection of $AB'$ and $BA'$. Let $\varphi:=\angle ASA'$. Then $\theta+2\varphi=180°$ always holds.

I haven't really worked out the details, but I'm sure that this helps to construct the segments $AB'$ and $BA'$ (and therefore $A'$ and $B'$).

Xaver
  • 586