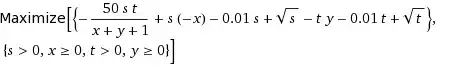0

I want to know if the Kuhn Tucker conditions can be used to identify a global maximum if one or more of the constraints is a strict inequality. What information would I need to answer this question?

Edit: The problem that motivated me to ask this is the following. Can Kuhn Tucker be applied here?

Doubt

glS
  • 6,818
bitter-sweet
  • 377
  • Yes, they can be used. Just treat the inequality as though it were not a strict inequality, apply your usual KKT, then discard any solutions that do not satisfy the strict inequality. – Zubin Mukerjee Jun 02 '16 at 20:36
  • @ZubinMukerjee Thanks! What is the justification for this, though? – bitter-sweet Jun 02 '16 at 20:38
  • I should add that there may be some problem with the fact that a function on an open set/interval may not actually have a maximum value. For example, $f(x)=1/x$ has no maximum on the open interval $(0,1)$, but any continuous function defined on a closed+bounded interval will have a maximum value (this is called the extreme value theorem) – Zubin Mukerjee Jun 02 '16 at 20:44
  • I messed around a little bit with your function and if you assume $s=t$ and $x=y$, then it is possible to find the maximum without KKT. @RobertIsrael – Zubin Mukerjee Jun 05 '16 at 05:33
  • @ZubinMukerjee Thanks. That is clear, but I can't make those assumptions in my problem. I posted this ques separately here, would be superb if you could take a look: http://math.stackexchange.com/questions/1810567/constrained-optimization-problem-of-4-variables – bitter-sweet Jun 05 '16 at 09:06

1 Answers1

1

Strict inequality constraints are never binding at a feasible solution (if they were, they wouldn't be strict inequalities). However, they can cause the problem to have no global maximum. What you might do is solve the problem with the strict inequalities replaced by non-strict inequalities. If this new problem has a global maximum where those strict inequalities are satisfied, then that is a global maximum of the original problem. If not, the original problem has no global maximum.

EDIT: Hmm, that's not quite always correct: it is true if the feasible region of the original problem is dense in the feasible region of the new problem. It is true if the new problem has a global maximum $p$ such that the gradients of the strict inequality constraints that are binding at $p$ are linearly independent.

Robert Israel
  • 448,999