probability question related to pattern in coin tossing

Question

If I toss a fair coin $n$ times, calculate the probability that no pattern HHTHTHH occurs.

Answer 1

I ended doing something very similar to Moron.

Define a Markov chain with states i=0..7 as follows. Given a full sequence of n coins, if the pattern has not yet appeared, find the maximum length of the last tosses (sequence suffix) that coincide with the begginning of the expected pattern, so that

   i =  length of matching suffix , if pattern has not appeared
   i = 7 otherwise

For example: HTTHTTTTHT : i=0 , HTTTTHHT i=3

It's easy to write down the transition probabilities. (i=7 would be a absorbent state), and the probability of being in state 7 in step n.

So your anwser would be $ P(n) = 1- p_7[n]$ where $p[n] = M^n p[0]$ where $M$ is the 8x8 transition matrix and $p[0] = (1,0,0,0,0,0,0,0)$ is the initial state. I doubt you'll get a simpler closed form answer.

One could get a very coarse approximate solution by assumming that the patterns starting at each position are independent (obviously a false assumpion), and get $ P(n) \approx (1-2^{-7})^{n-6}$ ($n \ge 7$)

UPDATE: some Octave/Matlab code to test the approximation (it seems to work better than I'd expected)

N=200;
% approximation
pa = (1-1/128).^((1:N)-6);
pa(pa>1)=1;
% transition matrix:
M = [ 1,1,0,0,0,0,0,0 ;
      1,0,1,0,0,0,0,0 ;
      0,0,1,1,0,0,0,0 ;
      1,0,0,0,1,0,0,0 ;
      0,0,1,0,0,1,0,0 ;
      1,0,0,0,0,0,1,0 ;
      1,0,0,0,0,0,0,1 ;
      0,0,0,0,0,0,0,2 ]/2;
p=[1,0,0,0,0,0,0,0];
p7=zeros(1,N);
p7(1)=1;
for n = 1:N
 p = p * M;
 p7(n) = 1 - p(8);
endfor
plot(7:N,p7(7:N),7:N,pa(7:N));

>>> pa(5:9)
ans =

   1.00000   1.00000   0.99219   0.98444   0.97675

>>> p7(5:9)
ans =

   1.00000   1.00000   0.99219   0.98438   0.97656

>>> pa(N-5:N)
ans =

   0.22710   0.22533   0.22357   0.22182   0.22009   0.21837

>>> p7(N-5:N)
ans =
   0.22717   0.22540   0.22364   0.22189   0.22016   0.21844

Answer 2

Construct a deterministic finite automaton which detects the regular expression $.*(HHTHTHH).*$ such that the sole accepting state $A$ always transitions to a state $B$, which always transitions to itself. The starting state is $S$.

This is basically a directed graph and we can find the transition matrix $P$, each row of which gives the probabilities of getting from one state (i.e. vertex) corresponding to that row, to the next states (one vertex corresponding to each column).

You basically need the entries corresponding to starting state $S$ and ending state $A$, from each of $P, P^2, P^3, \dots , P^n$ and add them up to get the probability that the pattern $HHTHTHH$ occurs (or more simply the $(S,B)$ entry of $P^{n+1}$ will do). Subtract that from $1$ and you are done.

The $(S,A)$ entry of $P^k$ gives the probability that we find the pattern exactly at the end of $k$ tosses, and no tosses before that.

Answer 3

I don't know about exact solution, but numeric approximation is $P(n)=1-e^{-\frac{n}{125}}$.

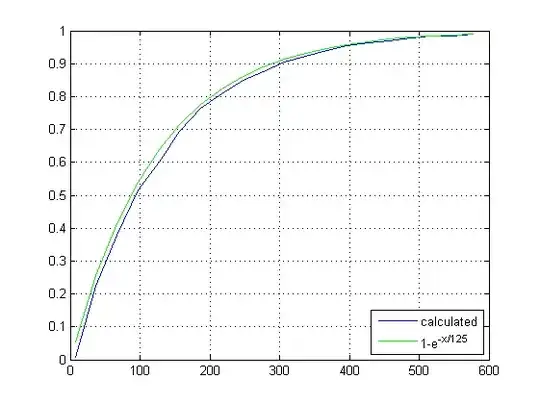
Matlab\Octave Code

function test_script_1()
x=7:30:600;
y=tsh([],5000,7:30:600);
er=@(p)sum(((p(1)+p(2)*exp(p(3)*x/500))-y).^2);
an=fminsearch(er,[0,0,0]);
anr=round(an);
disp(anr);
plot(x,y,x,anr(1)+anr(2)*exp(anr(3)*x));
legend('calculated','1-e^{-x/125}',4)
end
function result=tsh(a,b,n)
% HHTHTHH (H -> 1 , T -> 0)
if isempty(a)
    a=logical([1 1 0 1 0 1 1]);
end
if isempty(b)
    b=1000;
end
if isempty(n)
    n=100;
end
if any(size(n)>1)
    result=zeros(size(n));
    for pa=1:length(n)
        result(pa)=test_script_1(a,b,n(pa));        
    end
    return
end
la=length(a);
t=false(1,b);
for i=1:b
    v=raspr(0,1,n);
    for j=1:n
        if all(a==v(j:j+la-1))
            t(i)=true;
            break
        end
    end
end
result=nnz(t)/b;
end
function resu=raspr(a1,b1,s)
resu=round((b1-a1+1)*rand(1,s)+a1-0.5);
end

Somebody know why is that?