So I have this apparently smooth, parametrized function:
The function has a single parameter $ m $ and approaches infinity at every $x$ that divides $m$.
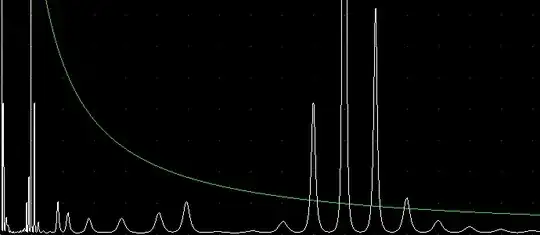
It is then defined for real $x$ apart from a finite set of arguments. The animation above shows plots of $f_{m}(x)$ (in white) for $x\in(0, 17>$, while each frame shifts $m$ by $0.05$ starting from $2$ and ending in $17$. In green plotted is a hyperbola $(x, {m\over x})$.
Explanation
Consider a lattice of integer-valued points $(a, b)$:
(the origin $(0, 0)$ is at the left-bottom corner of the picture)
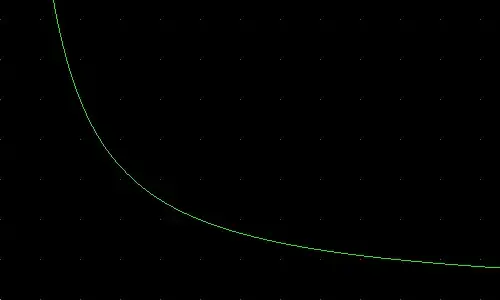
Let us draw a hyperbola $(x, {m\over x})$ for real $x$ and for $m = 10$.
It is trivial to observe that intersections of the hyperbola and the lattice lead us to factors of $m$, in this case, $10$. For example, the green curve above intersects red dots at $(2, 5)$ and $(5, 2)$.
Let us therefore define the function whose results were presented in the first animation:
$$f_{m}(x) = \sum_{a, b \in \mathbb{Z}} {1\over\lVert (x, {m\over x}) - (a, b)\rVert ^{3}} $$
What this function does intuitively:
- Choose a constant $m$ whose divisors you wish to seek.
- Given $x$, calculate point $(x, {m\over x})$ on the real plane.
- For every possible $(a, b)$ where $a$ and $b$ are integers, calculate distance of $(a, b)$ from $(x, {m\over x})$ and add inverse of cube of the result to the total sum.
Notice that if $x$ and $m\over x$ are integers (and therefore $x$ divides $m$), there exists an integer pair $(a, b)$ whose distance to ($x$, $m\over x$) is zero and when that happens, the series diverges due to addition of a $1 \over \lVert(0, 0)\rVert ^{3} $ term.
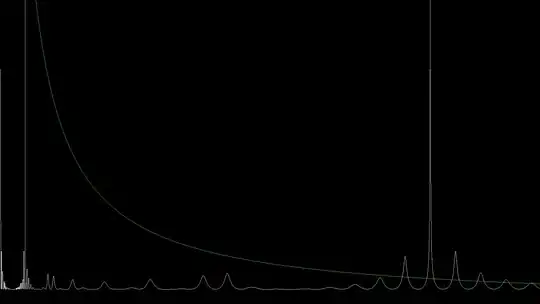
Plot of $f_{11}(x), x > 0$:
Notably, the function only ever approaches infinity at $x\in \{0, 1, 11\}$ ultimately indicating primality of $11$.
A little note: I've obtained the plots by coding a procedure that considers $(a, b)$ until distance inverses become less than some epsilon, in which case there is no point in further traversal.
Important update #1
I have updated the definition of $f_{m}(x)$ and replaced plots with ones generated by the new implementation, as it was previously using exponent of 2.
According to Daniel Fischer, $f_{m}(x)$ with exponent not bigger than $2$ in the denominator must necessarily diverge for every $x$ in its domain. I have therefore decided to use cubes.
Important update #2
It appears that in order to finely approximate $f_{m}(x)$, it is enough to simply sum inverses of distances to the four closest lattice points, instead of taking an infinite sum.
Let $H = (x, {m\over x} )$ (actual point on hyperbola)
Let $h = (\lfloor x \rfloor, \lfloor {m\over x} \rfloor)$ (the closest lattice point to the left-bottom)
Our new function is therefore
$$f_{m}(x) = {1\over \mathbf{d}(H, h) } + {1\over \mathbf{d}(H, h + (0, 1)) } + {1\over \mathbf{d}(H, h + (1, 0)) } + {1\over \mathbf{d}(H, h + (1, 1)) } $$
In fact, the plots look almost identical. Consider $f_{17}(x):$
For me, it appears to yield a perfectly acceptable estimate.
I believe it is especially worthy of our attention that the function looks like it remains smooth even in presence of floor function.
Questions:
- How can we qualify this function? Can we know that it is smooth? Analytic maybe?
- Is there a way to approximate this function without infinite series? Or maybe a simpler, exact formula? - Partially solved - four closest lattice points finely approximate the result while probably preserving smoothness.
- I've chosen square of the distance on the premise that it must converge equally well as the series $ \sum\limits_{n=1}^\infty {1 \over n^{s}}$ for $s > 1$. Is it actually the case that $f_{m}(x)$ must always converge for $x > 0$ and $x$ not dividing $m$? Solved - $f_{m}(x)$ must always diverge with the exponent not bigger than $2$ in the denominator.
- Is this function of any use? I know very well that the infinite series are far from efficient, but maybe there's an approximation that would sufficiently well predict factors? Or maybe, is it ultimately an obscure encoding of trial division?