The set of primes is recursively enumerable and can be generated by algorithms such as sieves and primality tests, e.g., the sieve of Eratosthenes, which uses trial division as a test. The definition of formula is very broad and only limited by the language it is expressed in. If $x=p_n$ is a well formed formula in a language that expresses the $n$'th prime then your question is trivially resolved. The more interesting question is whether a formula can be found for the primes which generates primes with the limitation of only using a particular set of operations. Some sets will permit a formula, others will not. For instance, if the only permissible operation is a nonconstant polynomial, there will be no such formula. Other answers have shown that expressions involving Mill's constant, exponentiation and the floor function can generate primes.
Formula for primes in terms of elementary arithmetic operations, $\lfloor x\rfloor$, sums and $\ln x$
Many algorithms can be rewritten algebraically in terms of the floor function, $\lfloor x \rfloor$, e.g., the aforementioned sieve of Eratosthenes. First, we may construct an indicator function for the primes. Define the modulo operator as $\operatorname{mod}(a,n)=a-n\left\lfloor \frac{a}{n}\right\rfloor$ and assume $x\in\mathbb{N_0},x\ge2$. Then, $\operatorname{mod}\left(x-1,i\right)$ is the remainder of the division of $(x-1)$ by $i$ and is $(i-1)$ iff $x$ is an integer multiple of $i$. This expression takes a value in $[0,i-1]$, therefore can be normalised to $\dfrac{\operatorname{mod}\left(x-1,i\right)}{i-1}$, which takes a value in $[0,1]$. The floor of this expression is then $0$ iff $i$ does not divide $x$. Therefore, $\textbf{1}_{i\, |\,x}=\left\lfloor \dfrac{\operatorname{mod}\left(x-1,i\right)}{i-1}\right\rfloor$ is the indicator function of whether $i\,|\,x$. When this expression is summed over $i=2,3,\ldots,\lfloor \sqrt{x}\rfloor$, it counts the number of divisors of $x$ between $2$ and $\sqrt{x}$. This is trial division and the largest integer that needs to be tested is $\sqrt{x}$. Thus, $\displaystyle \sum_{i=2}^{\left\lfloor\sqrt{x}\right\rfloor}\textbf{1}_{i\, |\,x}$ is $0$ iff $x$ has no divisors other than itself and $1$ and is in $(0,\left\lfloor\sqrt{x}\right\rfloor)$ otherwise. Similar to before, this can be normalised to $[0,1)$, subtracted from $1$, and its floor taken again to assign $0$ and nonzero values to either $0$ or $1$. Thus,
$$\left\lfloor 1-\frac{1}{\left\lfloor\sqrt{x}\right\rfloor}\sum_{i=2}^{\left\lfloor\sqrt{x}\right\rfloor}\textbf{1}_{i\, |\,x}\right\rfloor=\textbf{1}_{x\in\mathbb{P}}$$
is the indicator of whether $x$ is in the set of primes, $\mathbb{P}$. If $x\mapsto k$ and this indicator is summed over $k=2,3,\ldots,x$, it is then the prime counting function, $\displaystyle \pi (x)=\sum_{k=2}^x\textbf{1}_{k\in\mathbb{P}}$. The function $\left\lfloor\dfrac{2y}{x+y+1}\right\rfloor$ is the indicator of whether $0\le x<y$, for $x\in[0,\infty)$. Thus, $\left\lfloor\dfrac{2x}{\pi\left(r\right)+x+1}\right\rfloor$ indicates whether $\pi (r)$, the number of primes less than or equal to $r$, is strictly less than $x$. If this is summed from $r=2$ to $\infty$, it counts (up to a constant difference) how many $r$ have a prime count less than $x$. In other words, it represents the number at which the prime counting function is incremented. Therefore, the $x$'th prime is equal to $\displaystyle p_x=2+\sum_{r=2}^{\infty}\left\lfloor\frac{2x}{\pi\left(r\right)+x+1}\right\rfloor$. The upper limit of the sum can be brought down to a finite value, as $\pi(x)<2\left(\left\lfloor x\ln x\right\rfloor+1\right)$, so for all $r\ge 2\left(\left\lfloor x\ln x\right\rfloor+1\right)$, the terms in the sum are $0$.
Therefore, after putting this all together, we have a formula for all primes.
$$
p_x=
\small{2+\sum_{r=2}^{2\left\lfloor x\ln x\right\rfloor+2}\left\lfloor 2x\left(\sum_{k=2}^{r}\left\lfloor 1-\frac{1}{\left\lfloor \sqrt{k}\right\rfloor}\sum_{i=2}^{\left\lfloor\sqrt{k}\right\rfloor}\left\lfloor\frac{k-1-i\left\lfloor({k-1})/{i}\right\rfloor}{i-1}\right\rfloor\right\rfloor+x+1\right)^{-1}\right\rfloor}$$
Of course, this formula provides no real advantages over any algorithm implementing the sieve of Eratosthenes. A Desmos graph with each individual formula is available (here), while a graph with all formulas combined together is available (here) but bear in mind that it takes some time to compute. This method is partially adapted from On Formula to Compute Primes by Kaddoura and Abdul-Nabi.
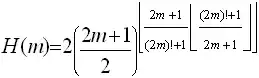
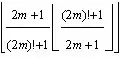
$$f(n) = \lfloor\theta^{3^n}\rfloor$$
which only generates primes, assuming the Riemann Hypothesis.
– Edward Evans May 30 '16 at 19:44