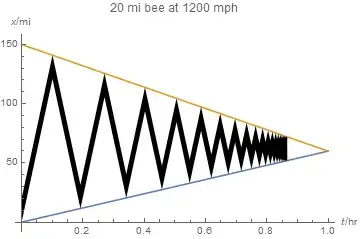
Here we derive some recurrence relations to determine position and times the bee meets one of the trains.
Scenario:
We consider the interval $[0,150]$ on the $x$-axis with train $A$ starting at time $t=0$ at position $x=0$ and train $B$ starting at the same time from $x=150$. Train A moves with $60$ mph towards B whereas train B moves with $90$ mph towards A.
The bee starts at time $t=0$ from $x=0$ towards $B$ with $120$ mph. It meets $B$ the first time at position $B_1$ after time $t_1$. At that time we denote the position of train $A$ with $A_1$. Then it turns around flies back to $A$ and meets $A$ at position $A_2$ after time $t_2$ while the train B is at position $B_2$ at that time. Then the bee turns around again and continues this dangerous game.
We denote the positions of the train A with $A_n$ and the positions of the train B with $B_n$, $n\geq 0$.
Note the bee meets the train $A$ at even positions $A_{2n}$ and it meets the train B at odd positions $B_{2n+1}$. The delta time between $A_{n}$ and $A_{n+1}$ is denoted with $t_{n+1}$ which is the same as the time between $B_{n}$ and $B_{n+1}$. We consider the following sequences
\begin{array}{rlllll}
\text{Train A: }&A_0=0,&A_1,&A_2,&\ldots &A_{n},\ldots\\
\text{Train B: }&B_0=150,&B_1,&B_2,&\ldots &B_{n},\ldots\\
\text{Delta times: }&t_0=0,&t_1,&t_2,&\ldots &t_{n},\ldots\\
\text{Bee: }&A_0=0,&B_1,&A_2,&\ldots&B_{2n-1},A_{2n},B_{2n+1},\ldots
\end{array}
We show the following is valid for $n\geq 0$
\begin{align*}
A_{2n}&=60\left(1-\frac{1}{3^n7^n}\right)\qquad&B_{2n}&=150-90\left(1-\frac{1}{3^n7^n}\right)\\
A_{2n+1}&=60\left(1-\frac{2}{3^n7^{n+1}}\right)\qquad&B_{2n+1}&=150-90\left(1-\frac{2}{3^n7^{n+1}}\right)\\
\\
t_{2n}&=\frac{5}{3^n7^n}\\
t_{2n+1}&=\frac{5}{3^n7^{n+1}}
\end{align*}
A first plausibility check shows
\begin{align*}
\lim_{n\rightarrow \infty}A_{2n}=\lim_{n\rightarrow \infty}A_{2n+1}
=\lim_{n\rightarrow \infty}B_{2n}=\lim_{n\rightarrow \infty}B_{2n+1}=60
\end{align*}
The trains will meet each other after one hour and since the speed of A is $60$ mph and it started from $x=0$ at $t=0$ its position is at $x=60$ after one hour. The same holds for $B$ since B moves with $90$ mph from $x=150$ and $150 - 90 = 60$.
Recurrence relations:
The bee meets the train A at delta time $t_{2n}$ at position $A_{2n}$ and then flies with $120$ mph towards the train B. We can calculate the next meeting point $B_{2n+1}$ with train B as
\begin{align*}
A_{2n}+120 t_{2n+1}&=B_{2n}-90 t_{2n+1}\\
t_{2n+1}&=\frac{1}{210}\left(B_{2n}-A_{2n}\right)\tag{1}
\end{align*}
The positions of A and B after delta time $t_{2n+1}$ are
\begin{align*}
A_{2n+1}=A_{2n}+60t_{2n+1}=\frac{5}{7}A_{2n}+\frac{2}{7}B_{2n}\tag{2}\\
B_{2n+1}=B_{2n}-90t_{2n+1}=\frac{3}{7}A_{2n}+\frac{4}{7}B_{2n}\tag{3}
\end{align*}
Similarly the bee meets the train B at odd indexed delta times $t_{2n+1}$ at position $B_{2n+1}$ and then flies with $120$ mph towards train A. We describe the next meeting position $A_{2n+2}$ with train A and obtain
\begin{align*}
B_{2n+1}-120 t_{2n+2}&=A_{2n+1}+60 t_{2n+2}\\
t_{2n+2}&=\frac{1}{180}\left(B_{2n+1}-A_{2n+1}\right)
\end{align*}
The positions of A and B after delta time $t_{2n+2}$ are
\begin{align*}
A_{2n+2}=A_{2n+1}+60t_{2n+2}=\frac{2}{3}A_{2n+1}+\frac{1}{3}B_{2n+1}\tag{4}\\
B_{2n+2}=B_{2n+1}-90t_{2n+2}=\frac{1}{2}A_{2n+1}+\frac{1}{2}B_{2n+1}\tag{5}
\end{align*}
From these equation we derive recurrence relations for odd and even $A_n$ in terms of $A_{n-1}$ and $A_{n-2}$ and we do the same for $B_n$.
We obtain from (2) - (5)
\begin{align*}
A_{2n+2}&=\frac{2}{3}A_{2n+1}+\frac{1}{3}B_{2n+1}\\
&=\frac{2}{3}A_{2n+1}+\frac{1}{3}\left(\frac{3}{7}A_{2n}+\frac{4}{7}B_{2n}\right)\\
&=\frac{2}{3}A_{2n+1}+\frac{1}{7}A_{2n}+\frac{4}{21}\left(\frac{7}{2}A_{2n+1}-\frac{5}{2}A_{2n}\right)\\
&=\frac{4}{3}A_{2n+1}-\frac{1}{3}A_{2n}
\end{align*}
and
\begin{align*}
A_{2n+1}&=\frac{5}{7}A_{2n}+\frac{2}{7}B_{2n}=\frac{5}{7}A_{2n}+\frac{2}{7}\left(\frac{1}{2}A_{2n-1}+\frac{1}{2}B_{2n-1}\right)\\
&=\frac{5}{7}A_{2n}+\frac{1}{7}A_{2n-1}+\frac{1}{7}\left(3A_{2n}-2A_{2n-1}\right)\\
&=\frac{8}{7}A_{2n}-\frac{1}{7}A_{2n_1}
\end{align*}
In the same way we derive for odd and even $n$ a representation of $B_n$ in terms of $B_{n-1}$ and $B_{n-2}$.
\begin{align*}
B_{2n+1}&=\frac{8}{7}B_{2n}-\frac{1}{7}B_{2n-1}\\
B_{2n+2}&=\frac{4}{3}B_{2n+1}-\frac{1}{3}B_{2n}
\end{align*}
With the help of (1) and (2) we can calculate $A_1$ and obtain a fully specified recurrence relation for $A_n$:
\begin{align*}
A_{2n+1}&=\frac{8}{7}A_{2n}-\frac{1}{7}A_{2n-1}\qquad\qquad n\geq 1\tag{6}\\
A_{2n+2}&=\frac{4}{3}A_{2n+1}-\frac{1}{3}A_{2n}\qquad\qquad n\geq 0\tag{7}\\
A_0&=0\\
A_1&=\frac{300}{7}
\end{align*}
$$ $$
Generating function for $A_{n}$:
We derive based upon the recurrence relation for $A_n$ a generating function $A(x)$ with
\begin{align*}
A(x)=\sum_{n= 0}^\infty A_nx^n
\end{align*}
Since we have according to (6) and (7) to respect even and odd part separately we do it in two steps and consider the even part
$(A(x)+A(-x))/2$ and odd part $(A(x)-A(-x))/2$ of the generating function accordingly. We start from (7) and replace for convenience $n$ with $n-1$. We derive from
\begin{align*}
A_{2n}&=\frac{4}{3}A_{2n+1}-\frac{1}{3}A_{2n}\qquad\qquad n\geq 1\\
\end{align*}
the generating function
\begin{align*}
\sum_{n= 1}^\infty A_{2n}x^{2n}&=\frac{4}{3}\sum_{n= 1}^\infty A_{2n-1}x^{2n}-\frac{1}{3}\sum_{n= 1}^\infty A_{2n-2}x^{2n}\\
\frac{A(x)+A(-x)}{2}-A_0&=\frac{4}{3}x\sum_{n= 0}^\infty A_{2n+1}x^{2n+1}-\frac{1}{3}x^2\sum_{n= 0}^\infty A_{2n}x^{2n}\\
&=\frac{4}{3}x\cdot\frac{A(x)-A(-x)}{2}-\frac{1}{3}x^2\cdot\frac{A(x)+A(-x)}{2}
\end{align*}
Noting that $A_0=0$ we obtain after some rearrangement
\begin{align*}
A(x)(x^2-4x+3)+A(-x)(x^2+4x+3)=0\tag{8}
\end{align*}
Now the odd part (6). We obtain
\begin{align*}
\sum_{n=1}^\infty A_{2n+1}x^{2n+1}&=\frac{8}{7}\sum_{n= 1}^\infty A_{2n}x^{2n+1}-\frac{1}{7}\sum_{n= 1}^\infty A_{2n-1}x^{2n+1}\\
\frac{A(x)-A(-x)}{2}-A_1x&=\frac{8}{7}x\cdot\frac{A(x)+A(-x)}{2}-\frac{1}{7}x^2\frac{A(x)-A(-x)}{2}
\end{align*}
with $A_1=\frac{300}{7}$ we obtain
\begin{align*}
A(x)(x^2-8x+7)-A(-x)(x^2+8x+7)=600x\tag{9}
\end{align*}
Combining (8) and (9) we can eliminate $A(-x)$ and obtain after some simplifications and partial fraction decomposition
\begin{align*}
A(x)&=\frac{300x(x+3)}{(x-1)(x^2-21)}\\
&=\frac{60}{1-x}+180\frac{2x+7}{x^2-21}\\
&=\frac{60}{1-x}+180\left(\frac{2\sqrt{21}-7}{42\left(1+\frac{x}{\sqrt{21}}\right)}
-\frac{2\sqrt{21}+7}{42\left(1-\frac{x}{\sqrt{21}}\right)}\right)\\
&=60\sum_{n= 0}^\infty x^n+\frac{30}{7}(2\sqrt{21}-7)\sum_{n= 0}^\infty \left(-\frac{1}{\sqrt{21}}\right)^nx^n\\
&\qquad\qquad\qquad-\frac{30}{7}(2\sqrt{21}+7)\sum_{n= 0}^\infty \left(\frac{1}{\sqrt{21}}\right)^nx^n\\
&=60\sum_{n= 0}^\infty x^n-\frac{60}{7}\sqrt{21}\sum_{n= 0}^\infty \frac{1-(-1)^n}{\left(\sqrt{21}\right)^n}x^n
-30\sum_{n=0}^\infty \frac{1+(-1)^n}{\left(\sqrt{21}\right)^n}x^n\\
&=60\sum_{n= 0}^\infty x^n-\frac{120}{7}\sum_{n\geq 0}\frac{1}{21^n}x^{2n+1}
-60\sum_{n=0}^\infty \frac{1}{21^n}x^{2n}\\
&=60\left(\sum_{n= 0}^\infty x^n-\sum_{n= 0}^\infty \frac{2}{3^n7^{n+1}}x^{2n+1}
-\sum_{n= 0}^\infty \frac{1}{3^n7^n}x^{2n}\right)\tag{10}
\end{align*}
We can now easily deduce the coefficients $A_n$ from (10).
\begin{align*}
A_{2n}&=60\left(1-\frac{1}{3^n7^n}\right)\\
A_{2n+1}&=60\left(1-\frac{2}{3^n7^{n+1}}\right)
\end{align*}
and the first part of the claim follows. According to (2) we obtain after some rearrangement
\begin{align*}
B_{2n}&=\frac{7}{2}A_{2n+1}-\frac{5}{2}A_{2n}\\
&=150-90\left(1-\frac{1}{3^n7^n}\right)
\end{align*}
and we get using (3)
\begin{align*}
B_{2n+1}&=\frac{3}{7}A_{2n}+\frac{4}{7}B_{2n}\\
&=\frac{3}{7}A_{2n}+2A_{2n+1}-\frac{10}{7}A_{2n}\\
&=2A_{2n+1}-A_{2n}\\
&=150-90\left(1-\frac{2}{3^n7^{n+1}}\right)
\end{align*}
which is the second part of the claim. Finally we obtain
\begin{align*}
t_{2n+1}&=\frac{1}{210}\left(B_{2n}-A_{2n}\right)=\frac{5}{3^n7^{n+1}}\tag{11}\\
t_{2n}&=\frac{1}{180}\left(B_{2n-1}-A_{2n-1}\right)=\frac{5}{3^{n}7^{n}}
\end{align*}
showing the last part of the claim is valid.
Epilogue: Of course we know the game is over after one hour and the distance travelled by the bee is $120$ miles. But we could also check it based upon the calculations above.
The total time the bee is flying is according to (11)
\begin{align*}
\sum_{n=0}^\infty\left(t_{2n+1}+t_{2n+2}\right)
&=\sum_{n=0}^\infty\left(\frac{5}{3^n7^{n+1}}+\frac{5}{3^{n+1}7^{n+1}}\right)\\
&=\left(\frac{5}{7}+\frac{5}{21}\right)\sum_{n=0}^\infty\frac{1}{3^n7^n}\\
&=\frac{20}{21}\frac{1}{1-\frac{1}{21}}\\
&=\frac{20}{21}\cdot\frac{21}{20}\\
&=1
\end{align*}
which is precisely one hour. The distance travelled by the bee is according to the last result
\begin{align*}
120t_1+120t_2+120t_3+\cdots=120\sum_{n=0}^\infty\left(t_{2n+1}+t_{2n+2}\right)= 120
\end{align*}
miles.