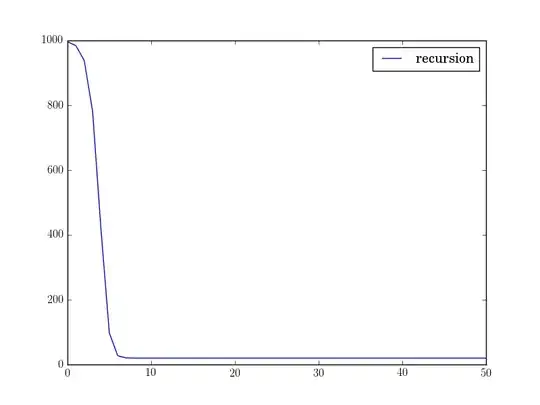
The corrected version of the question gives an easier result; the fixpoint to which the iteration proceeds is now expressible using the Lambert-W function only.
Let $a(0)=m-1$ , define always $b(k) = a(k)/m$, let $J=\exp(K)$ and iterate using the $b(k)$-version by
$\qquad b(k+1) = J^{b(k)-1} $
The fixpoint $\small t=\lim_{n \to \infty}b(n) $, if one exists, can be computed by
$ \qquad \begin{array}{rrlrl}
&&& t &= J^{t-1} \\
&&&-t J^{-t} &= - \frac1J \\
&&&-t K \cdot e^{-t K} &= -\frac KJ \\
&&&-t K &= W(- \frac KJ) \\
\to& t &= {W( -K e^{-K}) \over -K}
\end{array}$
and the fixpoint for $\small u=\lim_{n \to \infty}a(n) $ is then also $\small u=t \cdot m$ .
For $\small m=1000$ and $\small K=4$ I get
$\qquad \small \begin{array}{}
t \approx 0.01982740128177841 \\
u = t\cdot m \approx 19.82740128177841
\end{array}$
* Searching the interpolation-function*
1) First steps
First of all, when looking for an interpolating function, it is even better to define $c(n)$ as $c(n)=b(n)-1=a(n)/m-1$ and to rewrite the recursion on the $c(n)$ because this is a well known form:
$$ c(n+1) = J^{c(n)} - 1 \qquad \text{ where always } a(n) = (c(n)+1)\cdot m\tag 1$$
To define a function, which interpolates the $c(n)$ it is useful to remember, that such a function shall have different values wenn started at different values $c(0)$. So such a function should have two parameters: the initial value (which I'll call here formally $x$ or $x_0$) and the recursion-depth $h$ (which I denote according to the practice to call it the iteration-height of the power-tower , or better exponential-tower elsewhere). So we'll get a function $f(h,x)$ to denote the interpolated $c(h)$ when started at $c(0)=x = x_0$.
It is also convenient to denote $f(h,x_0)$ shorter as $x_h$ in the following formulae.
Then the problem of interpolating $x_h$ to fractional $h$ can be solved by creating exponential power series (and iterates of them) for a specific $h$.
Remember that $J=\exp(K)$ or $K=\log(J)$ by my first proposal above. Then the iteration height $h=1$ gives the power series in $x$ as
$$ x_1 = J^{x}-1 = Kx + (Kx)^2/2! + (Kx)^3/3! + ... \tag 2$$
For the iteration height $h=2$ we had
$$x_2 = Kx_1 + (K x_1)^2/2! + (K x_1)^3/3! + ... $$ where if we expand $x_1$ into its power series (and collect $x$ of like powers) get the series
$$\begin{array} {} x_2 &= K^2 x \\ &+ (1/2 K^4 + 1/2 K^3) x^2 \\& + (1/6 K^6 + 1/2 K^5 + 1/6 K^4) x^3 \\ & + O(x^4) \end{array}$$
If we try to continue for higher $h$ this we'll see that we get very complicated expressions for the coefficients at the powers of $x$. Of course we can try to find some formula for that coefficients depending on $h$ - and actually it is well known, that that coefficients are polynomials in $K$ depending on $h$.
But to arrive at a more handy notation we can observe, that at the terms of the series for $x_2$ we have that of powers of $x_1$ - respectively of $x_1$'s formal power series. This leads to the idea to introduce that whole mechanism in terms of matrix-notation, namely "Carleman-matrices":
1.a) Explanation of Carlemanmatrices with simpler function $\exp(x)-1$
We denote an infinitely sized vector of powers of $x$ as "Vandermonde-vector"
$$ V(x) = [1,x, x^2,x^3,...]$$
Then, with a vector $\small E_1 = [0,1,1/2!,1/3!,..]$ we get $\small V(x) \cdot E = \exp(x)-1 $ . Again with a certain vector $\small E_2 $ we get $\small V(x) \cdot E_2 = (\exp(x)-1)^2$. This can even be done by hand, and a software like Pari/GP can easily determine that coefficients in $\small E_2$ and even for higher powers of $\small \exp(x)-1$. Of course a vector $\small E_0 = [1,0,0,...]$ gives the formula $\small V(x) \cdot E_0 = (\exp(x)-1)^0 = 1$.
The idea is now to concat all those vectors $\small [E_0,E_1,E_2,...]$ to a matrix $E$ such that
$$ \begin{array}{} V(x) \cdot E & = [(\exp(x)-1)^0, (\exp(x)-1),(\exp(x)-1)^2,...] \\ V(x) \cdot E & = V(\exp(x)-1) \end{array} $$
The matrix $E$ is then said to be "the Carleman-matrix" for the map of $x$ to $\exp(x)-1$ and of course we see immediately that we can implement iterations to any iteration-"height" $h$ easily by
$$ V(x_0) \cdot E = V(\exp(x)-1) \\
V(\exp(x)-1) \cdot E = V(\exp(\exp(x)-1)-1) $$
or
$$ \begin{array} {}V(x_0) \cdot E^2 &= V(\exp(\exp(x)-1)-1) &= V((\exp(x)-1)^{°2}) \\
V(x_0) \cdot E^h &= V(...) &= V((\exp(x)-1)^{°h}) \end{array} $$
where the notation $ ()°h$ means the hth iteration. This shall then be generalized to fractional heights h and which can then be seen as a problem of fractional powers of the Carleman-matrix - and for cases, where the matrix is triangular like here this can be done by diagonalization.
2) Carleman-approach applied to $f(h,x)$
Of course in the above derivation for $\small E_1$, $\small E_2$ we do not want the function $\small \exp(x)-1$ but $\small f(1,x) = J^x-1 = \exp(Kx)-1$ and so we have to rewrite the above formulae where the logarithm $\small K=\log(J)$ is included to get $\small F_1$, $\small F_2$, $\small F_0$ and so on to arrive at the Carleman-matrix $F$ which provides
$$ V(x) \cdot F = V(J^x-1) = V(x_1) \\
V(x) \cdot F^h = V(x_h) \tag 4$$
Fractional powers of the matrix $F$ can now be found (if $\small K \ne 1$) by diagonalization: we solve for matrices $\small M,D,W$ such that
$$ F = M \cdot D \cdot W \qquad M \text{ triangular }, D \text{ diagonal}, W=M^{-1} \tag 5$$
Then also
$$ F^h = M \cdot D^h \cdot W \tag 6$$
and because $D$ is diagonal, fractional powers of $D$ are definable by fractional powers of the (scalar) values in the diagonal; so
$$ D^h = diag (\{(d_{k,k})^h\} \tag 7$$
is well defined for positive $d_{k,k}$ (which is the case here: $\small d_{k,k}=K^k$).
In my exercises I also normalize $M$ columnwise to have ones in the diagonal (which is always possible in diagonalization) so this becomes a Carlemanmatrix too. To have now the sought interpolation for the $c(h)=x_h$ we write
$$ V(x) \cdot (M \cdot D^h \cdot W) = V(x_h) $$ and because $x_h$ is in the second column of $V(x_h)$ we need only the second column of $W$ and can write
$$ x_h = V(x) \cdot M \cdot D^h \cdot W[,1] \tag 8$$
This gives expanded as power series in $\small x$ and coefficients in terms of polynomials in $\small K^h$ the final form:
$$ \tag 9 $$

3) Power series expansion of the interpolating function $f(h,x)$ and results
Of course it is useless to write down this expanded symbolic representation; one would only use a software system to compute this numerically, for instance Pari/GP which has also a diagonalization procedure.
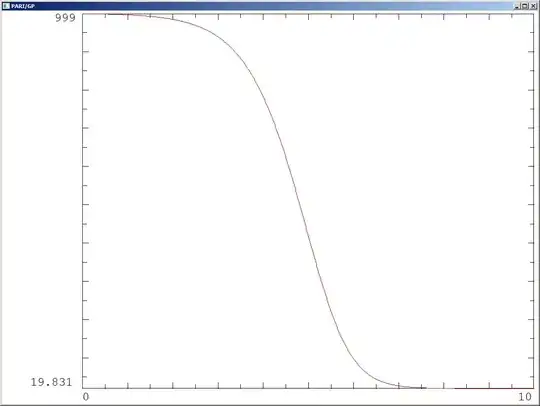
What I've got for $\small x_{0.5}$ when $\small m=1000,K=4$, $\small a(0)=m-1$ and $\small x_0 = c(0)= a(0)/m-1=-1/1000$ is
a(0) = 999
a(0.5) = 998.0013329778173
a(1) = 996.0079893439915
By the construction using the diagonalization and powers of $D$ we get a series, where the parameter $h$ is in the exponent of $K$. Since we have an example, where the initial value $a(0)$ resp. $x_0$ is a constant and $k$ has a known numerical value, we can even convert that series into a power series in $h$, which makes the implementation for this function $f(h,x_0)$ in a software even simpler.
Such a (well approximated(!)) powerseries for the interpolation of $a(n)$ when $a(0)=m-1=999$
$$a(h) = ( f(h,m-1)+1 ) \cdot m = 1000 \cdot f(h,999)+1000 $$
is
a(h)= 999.0000000000000 (10)
-1.385369918321135*h
-0.9589843868119868*h^2
-0.4419620583945484*h^3
-0.1523534905209286*h^4
-0.04178808785662870*h^5
-0.009446210118176247*h^6
-0.001788345571628710*h^7
-0.0002815129466004393*h^8
-0.00003469852606470614*h^9
-0.000002441465310162483*h^10
0.0000002768320051012997*h^11
0.0000001627165499006451*h^12
0.00000004386470378511849*h^13
0.000000009191769169195932*h^14
0.000000001635721799971140*h^15
0.0000000002499641412067852*h^16
3.137102721758781E-11*h^17
2.624644965932381E-12*h^18
-8.661931137401176E-14*h^19
-1.042873847809049E-13*h^20
-3.054037969497078E-14*h^21
-6.642022571747075E-15*h^22
-1.216917428014346E-15*h^23
-1.929073582659642E-16*h^24
-2.590632232952655E-17*h^25
-2.643188985117610E-18*h^26
-9.358555961832736E-20*h^27
4.551302748281239E-20*h^28
1.688715553335642E-20*h^29
3.998156282278988E-21*h^30
7.744676643907359E-22*h^31
+ O(h^32)
This gives the smooth curve
Original answer, referring to and based on a wrong formula is now deleted