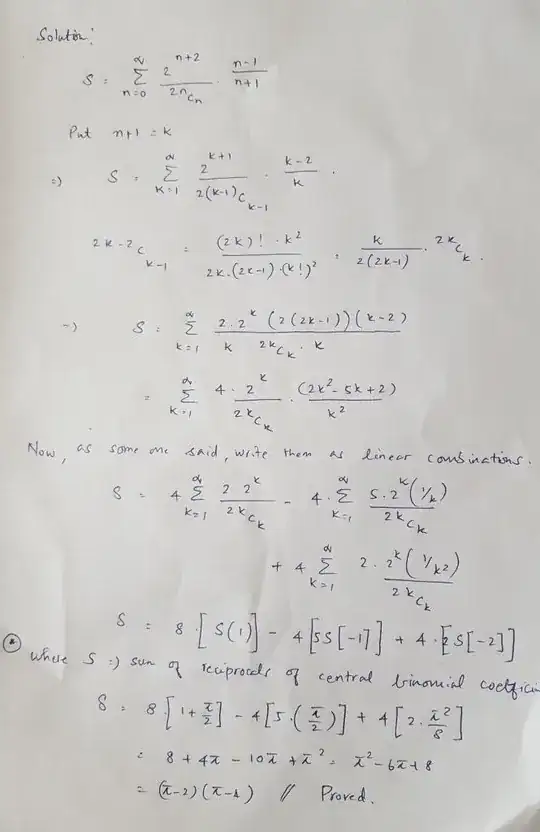8

Showing that

(1)

$$\sum_{n=0}^{\infty}\frac{2^{n+2}}{{2n\choose n}}\cdot\frac{n-1}{n+1}=(\pi-2)(\pi-4)$$

see here

(2)

$$(\arcsin(x))^2=\frac{1}{2}\sum_{n=1}^{\infty}\frac{(2x)^{2n}}{n^2{2n\choose n}}$$

Look very much similar to (1). How can I make the use of (2) to solve (1)?

Let try and differentiate (1) $$\frac{d}{dx}\arcsin(x))^2=\frac{d}{dx}\frac{1}{2}\sum_{n=1}^{\infty}\frac{(2x)^{2n}}{n^2{2n\choose n}}$$

$$\arcsin(x)\cdot\frac{1}{\sqrt{1-x^2}}=2\sum_{n=1}^{\infty}\frac{(2x)^{2n-1}}{n{2n\choose n}}$$ Getting close but not near yet

I am stuck, any help please?

Jack D'Aurizio
  • 353,855

3 Answers3

6

Hint. By using the Euler beta function, one has $$ \frac{2^{n+2}(n-1)}{{2n \choose n}(n+1)}=\frac{4(n-1)(2n+1)}{n+1}\int_0^1(2x(1-x))^ndx,\quad n \geq 0. \tag1 $$ Then, one may obtain $$\begin{align} &\sum_0^\infty\frac{2^{n+2}(n-1)}{{2n \choose n}(n+1)} \\\\&=\sum_0^\infty\frac{4(n-1)(2n+1)}{n+1}\int_0^1(2x(1-x))^ndx\\\\ &=\int_0^1\sum_0^\infty\frac{4(n-1)(2n+1)}{n+1}(2x(1-x))^ndx \:dx\\\\ &=\int_0^1\left(\frac{-40x^2+40x-12}{(1-2 x+2 x^2)^2}-\frac{4 \log(1-2 x+2 x^2)}{(1-x) x}\right)dx\\\\ &=\underbrace{\int_0^1\frac{-40x^2+40x-12}{(1-2 x+2 x^2)^2}\,dx}_{\large \color{blue}{8-6\pi}}+\underbrace{4\int_0^1-\frac{\log(1-2 x+2 x^2)}{(1-x) x}\,dx}_{\large \color{red}{\pi^2}} \\\\&=\color{blue}{8-6\pi}+\color{red}{\pi^2} \\\\&=(\pi-2)(\pi-4) \end{align} $$

as announced.

Some details.

Observe that $$ \sum_{n=0}^\infty(2n-3)y^n=\frac{5 y-3}{(1-y)^2},\quad |y|<1, \tag{A} $$ $$ \sum_{n=0}^\infty\frac1{n+1}y^n=-\frac{\log(1-y)}y,\quad |y|<1, \tag{B} $$ One has $$ \frac{4(n-1)(2n+1)}{n+1}=4(2 n-3)+\frac8{1+n} \tag{C} $$ then, using $(\text{A})$, $(\text{B})$ and $(\text{C})$ with $y:=2x(1-x)$ gives $$ \sum_0^\infty\frac{4(n-1)(2n+1)}{n+1}(2x(1-x))^n=\frac{-40x^2+40x-12}{(1-2 x+2 x^2)^2}-\frac{4 \log(1-2 x+2 x^2)}{(1-x) x} $$ One may classically integrate the fraction by parts. One may then rewrite the $\log$-term as $$ -\frac{4 \log(1-2 x+2 x^2)}{(1-x) x}=\frac{16}{1-u^2}\log \left(1-\frac{1-u^2}2\right) \tag{D} $$ with $u:=2x-1$, expanding in power series of $(1-u^2)$, integrating termwise to recognize a classic binomial series giving $\pi^2$.

Olivier Oloa
  • 120,989
  • I like your answer, but is there anyway you can break it down more or make it more simple for me, because I got a few more of these sums and I would like to prove it myself. I am not really following your proof due to my lack of knowledge but I do have some basic that I can follow your poof if you can simplify it more. If you can't then no worry sir. Thank you for your proof. –  May 29 '16 at 18:21
  • 1
    @mahdishafici I've edited my answer. Hoping it is OK now! – Olivier Oloa May 30 '16 at 16:34
4

It is worth considering that: $$ \frac{1}{\binom{2n}{n}}=\frac{n!^2}{(2n)!}=(2n+1)\cdot B(n+1,n+1)=(2n+1)\int_{0}^{1}x^n(1-x)^n\,dx \tag{1}$$ so: $$\sum_{n\geq 0}\frac{2^{n+2}}{\binom{2n}{n}}=\int_{0}^{1}\frac{4+8x(1-x)}{(1-2x(1-x))^2}\,dx = 4\int_{-1}^{1}\frac{3-y^2}{(1+y^2)^2}\,dy=8+2\pi\tag{2}$$ as well as: $$\begin{eqnarray*} \sum_{n\geq 0}\frac{2^{n+2}}{(n+1)\binom{2n}{n}}&=&4\int_{0}^{1}\int_{0}^{1}\frac{1+2xy-2x^2y}{(1-2xy+2x^2 y)^2}\,dx\,dy \\&=&8\int_{0}^{1}\frac{dx}{1-2x(1-x)}+2\int_{0}^{1}\frac{\log(1-2x(1-x))}{x(1-x)}\tag{3}\end{eqnarray*}$$ that is easy to compute through the substitution $y=2x-1$ as in $(2)$.

Jack D'Aurizio
  • 353,855
2

I have added a hand written image of the solution. The place where you need to take the results as is the sum of reciprocals of central binomial coefficients where people have given you articles to seive through. Goodluck.

enter image description here

Satish Ramanathan
  • 11,984