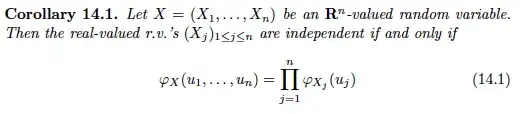3

Let $X, Y$ be two random variables such that for every $\alpha, \beta \in \mathbb{R}$, $$E[e^{it(\alpha X + \beta Y)}]=E[e^{it\alpha X}]E[e^{it\beta Y}]$$ for all $t\in\mathbb{R}$. Does it follow that $X$ and $Y$ are independent?

rmdmc89
  • 9,939
  • 1
    Another related question: http://math.stackexchange.com/q/191187/9464 –  May 27 '16 at 20:56

1 Answers1

4

The answer is YES. Let me introduce some notations first.

Suppose $X=(X_1,\cdots,X_n)$ is an $\mathbb{R}^n$-valued random variable (i.e., a random vector). The characteristic function for $X$, denotes as $\varphi_X(u)$, is a function from $\mathbb{R}^n$ to $\mathbb{R}$: $$\varphi_X(u):=E(e^{iu\cdot X}),\quad u\in\mathbb{R}^n$$ where $u\cdot X$ is the inner product in Euclidean space. In particular, when $n=1$, we have the characteristic function for random variables. Note also that $$ \varphi_X(u)=\varphi_{u\cdot X}(1)\tag{1} $$

The answer to your question follows directly from the following theorem (Probability Essentials by Jacod and Protter, Chapter 14):

enter image description here

To see how your question fits in this setting, let $Z=(X,Y)$ (these $X$ and $Y$ are random variables in OP) and $t=1$. Let $u=(\alpha,\beta)\in\mathbb{R}^2$. Then $$ E(e^{iZ\cdot u})=E(e^{i\alpha X})E(e^{i\beta Y}). $$

[Added due to the confusion in comments]
Note that one can interpret the question in OP in the language of characteristic functions as the following way:

If $$ \color{blue}{\forall (a,b)\in\mathbb{R}^2\ \forall t\in\mathbb{R}}\ \quad \varphi_{(a,b)\cdot (X,Y)}(t)=\varphi_{aX}(t)\varphi_{bY}(t)\tag{2} $$ then do we have that $X$ and $Y$ are independent?

Note carefully that the condition $(2)$ implies in particular that $$ \color{blue}{\forall (a,b)\in\mathbb{R}^2} \quad \varphi_{(a,b)\cdot (X,Y)}(1)=\varphi_{aX}(1)\varphi_{bY}(1)\tag{3} $$ which, by $(1)$, is equivalent to say that $$ \color{blue}{\forall (a,b)\in\mathbb{R}^2}\quad \varphi_{(X,Y)}(a,b)=\varphi_X(a)\varphi_Y(b).\tag{4} $$ In order to apply the theorem, note that $a,b$ here play the role of those $u_i$'s.

Note also that in $(2)$, $\varphi_{(a,b)\cdot(X,Y)}(t)$ is the characteristic function of the random variable $aX+bY$ when $a,b$ are fixed (and $t$ is the variable of the characteristic function). While in $(4)$, $\varphi_{(X,Y)}(a,b)$ is the characteristic function of the random vector $(X,Y)$ evaluated at $(a,b)$. $(1)$ tells you the relationship between these two objects.

  • I think that in the theorem, the $u_i$'s are the independent variables of the characteristic function, and in OP question $\alpha$ and $\beta$ are scalars. Moreover, the $t$ that you fix to 1 is the independent variable of the characteristic function in the OP's question. – Carlos H. Mendoza-Cardenas May 27 '16 at 16:39
  • No, the $u_i$'s are numbers in the theorem, not random variables. –  May 27 '16 at 16:44
  • 1
    @CarlosMendoza : $E[e^{i a X + i b Y}] = E[e^{iaX}]E[e^{ibY}]$ for every reals $a,b$ implies (by inverse Fourier transform of the characteristic function) that $f_{(X,Y)}(x,y) = f_X(x)f_Y(y)$ where $f_{(X,Y)}$ is the pdf of the random vector $(X,Y)$ (and when the pdf is not a function, you'll need some work but $f_{(X,Y)}(x,y) = f_X(x)f_Y(y)$ will still be true in the sense of distributions). finally this is exactly what means "$X,Y$ are independent" – reuns May 27 '16 at 17:36
  • (note : the characteristic function $\phi_X(a) = E[e^{i a X}]$ is the Fourier transform of the pdf $f_X(x)$, i.e. $\phi_X(a) = \int_{-\infty}^\infty f_X(x) e^{i a x} dx$) – reuns May 27 '16 at 17:38
  • @user1952009 If you prove that OP's equality implies that $f_{X,Y}(x,y) = f_X(x)f_Y(y)$ then you would answer the question. I keep thinking that Jack is misapplying the theorem for the characteristic function of a random vector. A characteristic function is, at the end of the day, a function, meaning that there must be one or more input (not random) variables that you could change in some range. In the theorem those variables are the $u_i$'s. In OP's question is $t$. $\alpha$ and $\beta$ are fixed (they are not input variables). – Carlos H. Mendoza-Cardenas May 27 '16 at 18:36
  • @CarlosMendoza: Can you point out exactly which line of my answer confuses you? –  May 27 '16 at 18:40
  • I see you keep thinking about the difference between $t$ and those $u_i$'s. Let me add something to my answer one more time. –  May 27 '16 at 18:43
  • Please take a look at my comment to the OP. – Carlos H. Mendoza-Cardenas May 27 '16 at 18:46
  • 2
    @CarlosMendoza : I'm explaining to you why $E[e^{iaX+ibY}] = E[e^{iaX}]E[e^{ibY}]$ for every reals $a,b$ implies $X,Y$ are independent. finally set $t=1$ in the OP question and voila. – reuns May 27 '16 at 19:13
  • @user1952009 I think that the main point that makes me disagree with you and Jack is the interpretation of the meaning of the quantifiers. For me, the "for every $\alpha$ and $\beta \in \mathbb{R}$" means that $\alpha$ and $\beta$ are arbitrary real constants. They are not input variables of the characteristic function. The only input variable is $t$, that by the way both of you are fixing to $1$. – Carlos H. Mendoza-Cardenas May 27 '16 at 19:33
  • @CarlosMendoza : the OP wrote : for every $a,b$ and for every $t$... – reuns May 27 '16 at 19:35
  • 2
    @CarlosMendoza: Note that if you are told $\phi_{X+Y}(t)=\phi_X(t)\phi_Y(t)$, this does not mean $X,Y$ are independent. The condition in OPs question is considerably stronger. Check this out: http://math.stackexchange.com/questions/376511/a-criterion-for-independence-based-on-characteristic-function

    A trivial example would be letting $X=Y$ where $X$ is Cauchy (the means add)

     – Alex R. May 27 '16 at 19:44
  • @CarlosMendoza: To put it in short, since the condition in OP is supposed to be true for every $t\in\mathbb{R}$, it is in particular true for $t=1$. This is exactly what I mean by "(2) implies (3)". –  May 27 '16 at 19:48
  • Could you apply the theorem without assuming $t=1$? – Carlos H. Mendoza-Cardenas May 27 '16 at 20:02
  • @AlexR. Great reference! However, in saz answer $\eta$ and $\xi$ are the input variables of the characteristic functions. I think that in the OP's question there is only one input variable: $t$. $\alpha$ and $\beta$ are arbitrary constants. What do you think? – Carlos H. Mendoza-Cardenas May 27 '16 at 20:13
  • @CarlosMendoza: No, saz's answer is exactly the same as OPs question (he implicitly implies that it must hold for all $t$). The condition holds for arbitrary $\alpha,\beta$ or $\eta,\xi$ (and $t$). To reiterate, OP says that the equality of expectations holds for arbitrary $\alpha,\beta,t$. This cannot be weakened. – Alex R. May 27 '16 at 20:16
  • 1
    @CarlosMendoza: The logic is as the following. Let $A$ be the condition in the question of OP, where $t$, in your language, is the input variable. Let $B$ be the condition of the theorem, namely, the particular case $t=1$. And let $C$ be the conclusion that $X$ and $Y$ are independent. By the theorem, $B$ implies $C$. Now $A$ implies $B$. (I'm not say that $A$ is equivalent to $B$.) Therefore, we conclude that $A$ implies $C$. –  May 27 '16 at 20:22
  • Thanks Jack for being patient, I finally got it. I am sorry for the inconvenience. I think that a tricky part is making $t=1$ (since the equality is true for every $t$, is true for $t=1$, finally!) and taking $\alpha$ and $\beta$ as your variables in the characteristic functions. That for me is the most valuable part of your answer at what makes it different from saz answer in the reference that Alex shared. In that sense, I suggest starting your answer with that considerations. That would make it clearer. – Carlos H. Mendoza-Cardenas May 27 '16 at 20:42
  • @CarlosMendoza : and forget your input variables... if $f$ and $g$ are two functions $\mathbb{R} \to \mathbb{R}$ then $f=g$ means literally $\forall x \in \mathbb{R}, f(x) = g(x)$.. – reuns May 27 '16 at 20:52