The scenario in the OP is not possible. The following (informal) proof has nothing to do with my previous "answer" so I thought I'd make a new one.
The proof relies on the following 2 facts:
- The minimum number of Rows Needed to ensure that at least one row has a winning combination depends on the number of Calls, and increases monotonically as Calls decreases from 25 to 5.
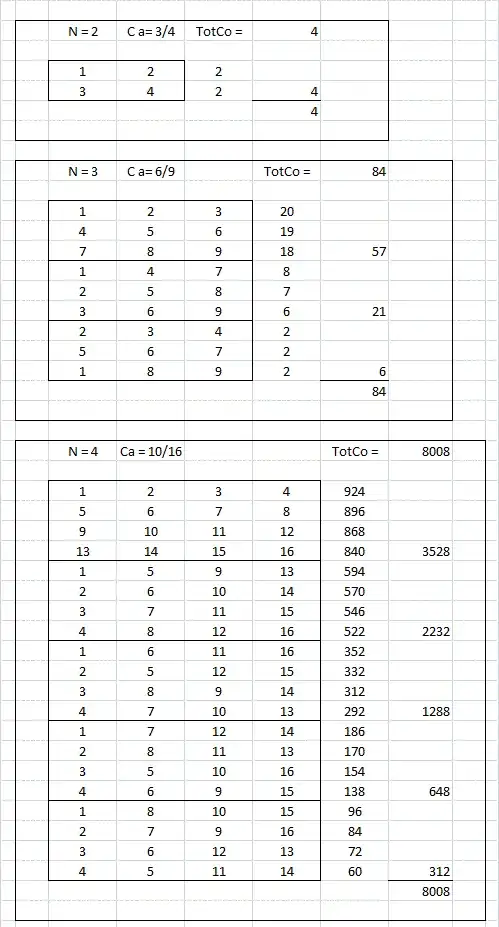
- Already at Calls = 20, Rows Needed = 30 (= 6 cards). As the OP suggested that it was possible with Calls = 15 to have Rows Needed = 25, the OP is disproved.
Re. 1
If Calls = 25, all numbers have been called and just 1 number is needed to assure a winning combination. As the minimum unit we are working with is rows, just 1 row is needed. If Calls = 24, 1 number has not been called. This 1 number could be in our first row, so we need at least 2 rows of unique numbers. If Calls = 23, 2 numbers have not been called and we need at least 3 rows of unique numbers. For Calls = 22, 4 rows are needed. For Calls = 21, 5 rows are needed.
For Calls = 20 we can no longer introduce a new row of unique numbers, as all 25 unique numbers have been used in the first 5 rows (= the first card). However, it is clear that more rows are needed as 5 numbers have not been called and there could be one such number in each of the 5 rows we already have. It should also be clear that for Calls < 20, even more rows are needed. The maximum Rows Needed occurs when Calls = 5, at which point we need all possible combinations of 5 numbers selected from 25 numbers or $\frac{25!}{(20!)(5!)}= 53,130$ rows.
Re. 2
At Calls = 20, there are 5 numbers which have not been called. It is therefore not enough to have 5 rows of unique numbers as there could be one uncalled number in each row. So how many rows are needed to ensure a winning combination?
We can guarantee a winning combination if we can show that at least one row in a card has 2 uncalled numbers. If one row has 2 uncalled numbers, there are only 3 uncalled numbers left, but we have 4 rows left on the card. That means at least one row has only called numbers.
So how many cards are needed to show that at least one row will have 2 uncalled numbers?
Suppose the number 1 is uncalled. If we have enough cards such that we can be sure that 1 has been together with every other number, then we know that at least in one of those cards, 1 will be together with another uncalled number. This is possible with 6 cards (= 30 rows). In fact, it is possible with 30 rows, no matter what the initial number (1 in this case). With 30 rows (= 6 cards) every number can be in a row with every other number and therefore at least one row in a card has a row containing only called numbers. Below is an example:
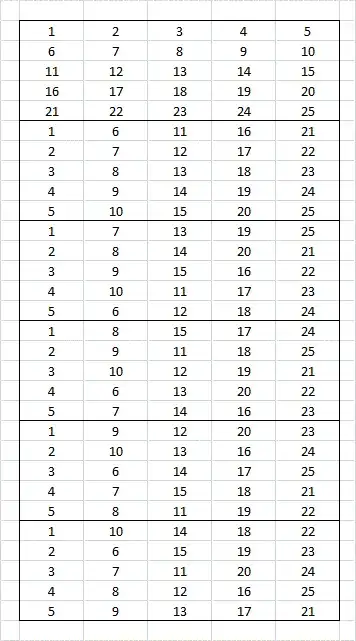
Edited to add
One needs at least 30 rows because there are 25 numbers. There are therefore 24 other numbers for any given number. A given number can only occur in one row in a card. It can therefore only be together with 4 new numbers in every card. With 4 new numbers per card, one needs at least $\frac{25-1}{4}=6$ cards.