8

I'm reaching back into my high school days trying to remember one of the rules about Karnaugh Maps. I have an 8 variable input, and I remember that I should try and make the selections a big as possible. However, I vaguely remember that if I have a selection, that the number of $1$'s for a variable must equal the number of $0$'s for the same variable if it is to cancel out.

When dealing with 4 variable tables, this is not a problem, but when I move to 8, I can get a single selection that has columns $0010$, $0110$, $0111$, $0101$, $0100$, $1100$, $1101$ and $1111$ selected.

As you can see, the bit 3 (msb) has 5 $0$s and 3 $1$s, bit 2 has 1 $0$s and 7 $1$s, bit 1 and 0 have 4 of each. My questions are:

  1. Is this a valid single selection?
  2. If this is a valid single selection, how do I handle it?
  3. If not a valid single selection, why not? What are the rules that stipulate what a valid single selection is? What is the meaning behind those rules?

I understand that when a bit is constant, it is used. When there are equal numbers of $1$s and $0$s, they cancel each other out. So what is done when there unequal number of $1$s and $0$s?

EDIT

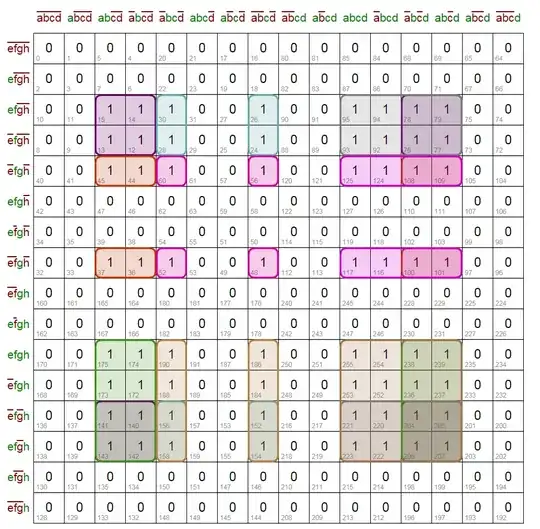
For those of you who didn't understand what I was talking about, here is a 8 variable Karnaugh map:

enter image description here

The top header shows the numeric and the symbol representation of the values. I've not done the same for the left side header, but assume that they represent 4 other independent variables E, F, G, and H, though it is really irrelevenat.

Assume that all that are marked $1$ are true values and those not marked are false.

The $1$'s represent an 8x8 selection matrix, which by my understanding is a valid selection. Note that this could easily be an 8x1, 8x2, 8x4, 8x8 or 8x16 matrix located as a single grouping anywhere in the column specified. This is just an example.

Community
  • 1
Adrian
  • 191
  • There is a non-geometric method for simplifying Boolean sums called the "consensus" method (or the like) which is better to use when there are many variables. – coffeemath May 23 '16 at 22:24
  • @coffeemath, good to know. I'll look it up. However, I thought that Karnaugh maps could handle a 8 variable item, and would like to know the rules for this. – Adrian May 23 '16 at 23:03
  • So there is no answer for this? – Adrian May 31 '16 at 05:52
  • Can you explain how your binary numbers work for the column selection? I count eight binaries each of length 4, for 32 possible bits, and since $32=2^5$ I would have thought that was the five variable case. – coffeemath May 31 '16 at 17:11
  • @coffeemath, each bit represents a truth value. It would be like $A \wedge \bar{B}$ is being represented by $10$. I listed 8 columns, so that is 8 groups of 4 binary variables. – Adrian May 31 '16 at 17:18
  • If you implement an equality operator to allow in the algebra this will go much smoother. Are you allowed to do that? – mathreadler Jun 04 '16 at 12:45
  • @mathreadler, I'm not sure what you mean. Are you answering the question or giving an alternative way to solve the question? – Adrian Jun 09 '16 at 00:22

2 Answers2

6

Your "Karnaugh Map" is not a valid Karnaugh map, because the ordering of the rows and columns does not follow the symmetry rules. Look at the example shown below.

While Karnaugh maps are mainly used upto six variables, Mahoney extended the construction to more variables using reflection symmetries. An article explains some details. However, I have never seen this being used in practice.

Your sample depicted as a map for 8 variables looks as follows:

enter image description here

This example was created using a home-grown tool similar to this website.

For 8 variables, there are 256 cells in the map. This is not really practical for human inspection.

The trick of Karnaugh maps is to quickly find adjacent minterms which only differ in one input variable and can thus be merged into a term with fewer inputs. However, as you can see from the example, this gets out of hand if the number of terms becomes too big.

In a Mahoney map, "1" cells can be merged into a common block, if they can be folded onto each other in terms of a reflection symmetry.

To minimize an expression with more than a handful of variables, tools like Espresso or Boom are available for free. These are PLA minimizers which strive to reduce a list of minterms.

In case your original expression is a Boolean formula rather than a set of minterms, you might have a look at tools like ABC, bc2cnf or Logic Friday.

As a classic text on the topic, I can highly recommend:

R. Brayton, G. Hachtel, C. McMullen and A. Sangiovanni-Vincentelli: Logic Minimization Algorithms for VLSI Synthesis Kluwer Academic Publishers, 1984.

Your expression is equivalent to

b!cf!g + bdf!g + b!cfh + bdfh + !ac!df!g + !ac!dfh + b!c!eg!h + bd!eg!h + !ac!d!eg!h

In the Karnaugh/Mahoney map shown above, this is visualized as nine blocks (drawn in different colors) which together cover the 64 minterms.

The eight ABCD columns can be simplified to a sum of three terms

b!c + bd + !ac!d

             cd
       00  01  11  10
      +---+---+---+---+
   00 | 0 | 0 | 0 | 1 |
      +---+---+---+---+
   01 | 1 | 1 | 1 | 1 |
ab    +---+---+---+---+
   11 | 1 | 1 | 1 | 0 |
      +---+---+---+---+
   10 | 0 | 0 | 0 | 0 |
      +---+---+---+---+

The same can be done with the eight EFGH columns. Therefore, your expression is a conjunction of 3x3 terms resulting in 9 terms.

Axel Kemper
  • 4,943
  • Although interesting and informative about what tools are out there, this isn't answering the question. – Adrian Jun 02 '16 at 19:25
  • There you go. I've added an example to the OP to try and clarify. – Adrian Jun 02 '16 at 22:37
  • According to your weblink, it is not valid as a single selection, and that is what I'm asking about. – Adrian Jun 03 '16 at 12:55
  • Thus the reason for my question. 1. Is this a valid selection? Answer: No, not in one selection. or Yes, but not in one selection. I've tried to add more explicitly that I want a WHY answer, but it was supposed to be implied by 2. If this is a valid selection, how do I handle it? – Adrian Jun 03 '16 at 22:20
  • Again interesting, but still doesn't answer the question: Why is it not a valid single selection? What are the rules governing a valid single selection? – Adrian Jun 04 '16 at 14:59
0

Hint For real big maps you could do a separable Haar filtering of a multidimensional array (followed by downsampling). The logical expression $$([1,1]*f = 2) \& ([1,-1]*f = 0)$$ is a condition that tells us "here is something we can keep going on" our signal $f$. We probably want to do a depth-first search noting the "coordinates" of all vanishing 1 of the above condition.

mathreadler
  • 25,824