3

Let $N=a^2+nb^2$ with $\gcd(a,b) =1$ and $n \in \mathbb{Z^+}$. If $N=xy$ where $x$ and $y$ are relatively prime numbers, in what condition can $x$ and $y$ be also written in the same form as $N$ (i.e, $c^2+nd^2$) ? How can we prove it?

The above statement is true for sum of two squares (i.e, the case $n=1$), which has been proved by Fermat and Euler $($Here $ \text{is Euler's proof, see Proposition} \ 4)$ using Infinite Descent and Brahmagupta's Identity. But can it be generalized?

Any help will be appreciated.
Thanks.

Martin Sleziak
  • 53,687
Henry
  • 5,549
  • See https://proofwiki.org/wiki/Brahmagupta-Fibonacci_Identity#Proof – lab bhattacharjee May 20 '16 at 09:41
  • Brahmagupta's Identity is the converse of what you are saying. Your statement is indeed true for the sum of two squares, but not for that reason. Now to the point: say, $n=5$. Then $6=1^2+5\cdot1^2$ and $6=2\cdot3$, but $2$ and $3$ are obviously not of the form $a^2+5b^2$. So not all $n$ are good. – Ivan Neretin May 20 '16 at 09:50
  • 2
    I believe this has something to do with $\mathbb Q(\sqrt{-n})$ being or not being a unique factorization domain, but here I'm stepping outside my expertise. – Ivan Neretin May 20 '16 at 10:13
  • What is $N$? Do you mean the same form as $\lambda$? – almagest May 20 '16 at 10:20
  • 2
    @IvanNeretin You are right. Letting $\alpha=a+b\sqrt{-n}$, we have $\lambda=N(\alpha)=\alpha\overline{\alpha}$ ($N$ is the complex number norm). Since $x,y$ stay relatively prime in $\Bbb Z[\sqrt{-n}]$ (because they satisfy $xx'+yy'=1$ for some integers), we get $\alpha\overline{\alpha}=xy$. Assuming unique factorization and using the fact that $x,y$ are real we can now deduce that they can be written as $x=\beta\overline{\beta}=N(\beta),y=\gamma\overline{\gamma}=N(\gamma)$. – Wojowu May 20 '16 at 13:26
  • @IvanNeretin I know what is the identity, but it can be used to prove my statement for $n=1$. Leonhard Euler proved it using the identity and infinite descent as a Proposition (See Proposition 4) to proving Fermat's two square theorem. – Henry May 20 '16 at 13:32
  • @labbhattacharjee Apparently, you didn't get my question. I know what is the identity and its proof, but I'm asking whether for a number of the same form, are its factors also of that form (when $\gcd(a,b)=1$)? – Henry May 20 '16 at 13:34
  • @labbhattacharjee For instance, the identity can be used to prove my statement for $n=1$. Leonhard Euler proved it using the identity and infinite descent as a Proposition (See Proposition 4) to proving Fermat's two square theorem. – Henry May 20 '16 at 13:35
  • @labbhattacharjee I've added more details to the question. Can you please give some insights? Thanks. – Henry May 20 '16 at 13:43
  • @IvanNeretin I've added more details to the question. Can you please give some insights to the question based on the new information? Thanks. – Henry May 20 '16 at 13:44
  • What insights? I gave you the tentative answer and Wojowu explained why it was right. Read about the unique factorization domains and the Heegner numbers. – Ivan Neretin May 20 '16 at 14:46
  • @IvanNeretin Thanks for that, I'll read about UFD. But I was talking about an elementary solution similar to the case $n=1$ for which I have provided a link in the question. – Henry May 20 '16 at 15:35
  • Whether or not that elementary solution can be generalized, I don't know. – Ivan Neretin May 20 '16 at 15:49
  • @IvanNeretin Okay. Thanks for your help though :) – Henry May 20 '16 at 16:09

1 Answers1

4

This is true when $a^2 + n b^2$ is of class number one ( well, the form class number of the discriminant $-4n$). I refer to the number of (equivalence classes of) primitive binary quadratic forms with that discriminant, $-4n.$ Even in this case, we need to be cautious when there are also imprimitive forms of that discriminant. This is all in Dickson's little book, page 91

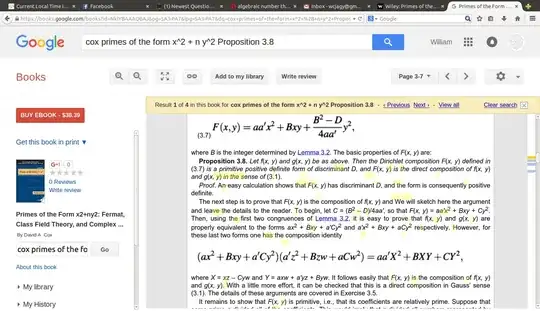
An easy example would be $x^2 + 6 y^2,$ where the other class of this discriminant is $2 x^2 + 3 y^2.$ Now, $ 3 \cdot 11 = 33 = 9 + 6 \cdot 4.$ Neither of $3,11$ can be expressed as $x^2 + 6 y^2.$ However, in accordance with Dickson, $11 = 2 \cdot 4 + 3,$ and $3 = 2 \cdot 0 + 3.$ This example even gives a formula, $$ (2u^2 + 3 v^2)(2x^2 + 3 y^2) = (2ux+3vy)^2 + 6 (uy-vx)^2 $$ There are always such formulas, this is Gauss composition, but no guarantee that the whole thng will be pretty. The most elegant ones happen when we have already written the forms ready for Dirichlet's presentation of composition. This can be found, for example, in the book by Cox, Primes of the Form $x^2 + n y^2.$

enter image description here

Dirichlet on composition: we usually write the forms of discriminant $-44$ as $x^2 + 11 y^2,$ $3 x^2 + 2 xy + 4 y^2,$ $3 x^2 - 2 xy + 4 y^2.$ However, the first is $SL_2 \mathbb Z$ equivalent to $27 x^2 + 8 xy + y^2,$ the second form to $3 x^2 + 8 xy + 9 y^2,$ the third (its "opposite" class) to $9 x^2 + 8 xy + 3 y^2.$ And composition comes out well: $$ (3 x^2 + 8xy + 9 y^2)(9 z^2 + 8zw + 3 w^2) = 27 X^2 + 8XY + Y^2, $$ where $$ X =xz-yw, \; \; Y=3xw+9yz+8yw $$ This is on page 49 in the first edition of Cox, which had a typo in the formula for $X.$ Corrected in the second edition, see if I can paste in an excerpt.

enter image description here

Will Jagy
  • 139,541
  • I suppose you mean the class number of the integer ring of $\Bbb Q(\sqrt{-n})$, not the class number of $a^2+nb^2$. – Wojowu May 20 '16 at 17:24
  • @Wojowu What I meant is the count of classes of quadratic forms of discriminant $-4n.$ The comparison with your concept is done well in Buell, Binary Quadratic Forms. See also http://math.blogoverflow.com/2014/08/23/binary-quadratic-forms-over-the-rational-integers-and-class-numbers-of-quadratic-%EF%AC%81elds/ – Will Jagy May 20 '16 at 17:29
  • I was just pointing out that the term "class number" usually refers to a number field, not a quadratic form. If I'm mistaken about that, then never mind. – Wojowu May 20 '16 at 17:31
  • 1
    @Wojowu if you have not seen the part from Cox about Dirichlet composition you might like it. The number field viewpoint took over so completely that most mathematicians do not know the way binary quadratic forms were treated. After years on this site, I am pretty sure that a week of quadratic forms would be a valuable addition to a beginning number theory course; computations are so much easier. – Will Jagy May 20 '16 at 18:03
  • You're not Mike Webb, but I'd still scrutinize tabs on screenshots before posting them. – Mr. Brooks May 23 '16 at 20:56
  • 1
    I agree with Will Jagy who regrets that "the number field viewpoint took over so completely that most mathematicians do not know the way binary quadratic forms were treated". I must confess that I belong to this "ignorant tribe", and even after learning of the existence of the book of David Cox, I thought that the local-global principle of CFT could give information in the style "p must split into the product of 2 principal primes". But then I took a (diagonal) look at the book and found that everything was in there, including the use of complex multiplication. – nguyen quang do May 24 '16 at 13:41
  • My conclusion is : there is no way to improve upon Cox, and my tentative answer (even after fixing an error) must stay where it belongs - in limbo. – nguyen quang do May 24 '16 at 13:46