How to Find the Minimum Value for $\frac{\tan x}{x}$ (piecewise defined)?

Question

$$F (x) = \begin{cases} \displaystyle \frac{\tan(x)}{x} & x \not=0 \\ 1 & x=0 \end{cases} $$

How do I prove that there is a local minimum at $x=0$?

Answer 1

The first derivative test seems easiest to apply here. For $x>0$, $$\frac d{dx}\frac{\tan x}x=-\frac1{x^2}\tan x+\frac1x\sec^2x=\frac{x-\sin x\cos x}{x^2\cos^2x}$$ By a geometric argument you were shown, around the time you learned the derivatives of the trigonometric functions, that for $0<x<\frac{\pi}2$, $\sin x\cos x<x<\tan x$. For this reason we know that $$\frac d{dx}\frac{\tan x}x=\frac{x-\sin x\cos x}{x^2\cos^2x}>0$$ for $0<x<\frac{\pi}2$. It follows that $-(x-\sin x\cos x)=(-x)-\sin(-x)\cos(-x)<0$ for $0<x<\frac{\pi}2$ so that $x-\sin x\cos x<0$ for $-\frac{\pi}2<x<0$, so $$\frac d{dx}\frac{\tan x}x=\frac{x-\sin x\cos x}{x^2\cos^2x}<0$$ for $-\frac{\pi}2<x<0$. Since $$\lim_{x\rightarrow0}\frac{\tan x}x=\lim_{x\rightarrow0}\left(\frac1{\cos x}\frac{\sin x}x\right)=(1)(1)=1=F(1)$$ Then $F(x)$ is continuous at $x=0$ and $F^{\prime}(x)<0$ for $-\frac{\pi}2<x<0$ and $F^{\prime}(x)>0$ for $0<x<\frac{\pi}2$ it follows that $F(x)$ has a relative minimum at $x=0$ by the first derivative test.

EDIT: Here is the geometric argument I was alluding to. Consider this figure:

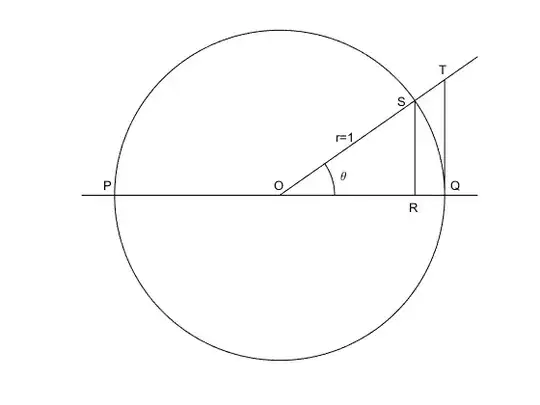
It may be rather hard to read my crude diagrams, but it is supposed to depict the unit circle centered at $O$. Sector $OQS$ of the circle has area $$A(OQS)=\frac{\theta}{2\pi}\pi(1)^2=\frac12\theta$$ Where we have assumed that the area of a sector is proportional to its central angle, here $\theta$, and used the mensuration formula for the area of a circle, $A=\pi r^2$. Then right triangle $ORS$ lies entirely within sector $OQS$ and its area is $$A(ORS)=\frac12\cos\theta\sin\theta$$ where we have use the mensuration formula $A=\frac12(\text{base})(\text{height})$ for the area of a triangle. Finally the sector $OQS$ itself lies entirely within right triangle $AQT$ with area $$A(OQT)=\frac12(1)\tan\theta=\frac12\tan\theta$$ Since one is contained within another, $$A(ORS)<A(OQS)<A(OQT)$$ Or $$\frac12\sin\theta\cos\theta<\frac12\theta<\frac12\tan\theta$$ I thought that this was the argument made to show how to differentiate trigonometric functions through $$\begin{align}\frac d{dx}\sin x&=\lim_{h\rightarrow0}\frac{\sin(x+h)-\sin x}h=\lim_{h\rightarrow0}\frac{\sin x\cos h+\cos x\sin h-\sin x}h\\ &=\lim_{h\rightarrow0}\frac{\sin x(1-2\sin^2(h/2))+\cos x\sin h-\sin x}h\\ &=\lim_{h\rightarrow0}\frac{\sin h}h\cos x-\lim_{h\rightarrow0}\frac{\sin(h/2)}{(h/2)}\sin(h/2)\sin x\\ &=(1)\cos x-(1)(0)\sin x=\cos x\end{align}$$ Because through the geometric argument you knew that $$\cos x<\frac{\sin x}x<\sec x$$ And since $$\lim_{h\rightarrow0}\cos x=\lim_{h\rightarrow0}\sec x=1$$ It follows by the squeeze theorem that $$\lim_{h\rightarrow0}\frac{\sin x}x=1$$

Answer 2

Since you can rewrite $F$ as $$F(x)=\int_0^1{1\over\cos^2(\tau x)}\>d\tau\geq1=F(0)\qquad\left(-{\pi\over2}<x<{\pi\over2}\right)$$ the function $F$ takes its minimum in the interval $\>(-{\pi\over2},{\pi\over2})\ $ at $x=0$.

Answer 3

(In what follows I am assuming that the domain here is $-\frac{\pi}{2} <x < \frac{\pi}{2}$)

For $x<0$, $\tan x < 0$, therefore $ \frac{\tan x}{x} >0$.

Likewise, for $x>0$, we have $\tan x > 0$, and again $\frac{\tan x}{x} > 0$.

Hence in order to show that the modified piecewise version of $\frac{\tan x}{x}$ has a minimum at $x=0$, it suffices to show that $|\tan x| > |x|$ for all $x \in (-\frac{\pi}{2},0) \cup (0, \frac{\pi}{2})$.

This is because this condition would imply that $\frac{\tan x}{x} >1$ for those values.

This is clear from the following graph:

(again, I am assuming that $x \in(-\frac{\pi}{2},0)\cup (0, \frac{\pi}{2})$)

since the graphs do not intersect. (Note: $\frac{\tan x}{x} >1 \iff \tan x > x$)

For a better graphical proof of the fact that $$\tan x > x, \quad x \in (0, \frac{\pi}{2}$$ see here: http://mathrefresher.blogspot.com/2006/08/sin-x-x-tan-x-for-x-in-02.html

or here: Why $x<\tan{x}$ while $0<x<\frac{\pi}{2}$?

or: https://www.quora.com/How-do-I-prove-this-displaystyle-frac-tan-x-x-gt-frac-x-sin-x-when-x-in-left-0-frac-pi-2-right

or: https://www.quora.com/How-do-I-prove-that-sin-x-x-tan-x-for-all-x-in-left-0-frac-pi-2-right

or: https://answers.yahoo.com/question/index?qid=1006050131519

or: https://answers.yahoo.com/question/index?qid=20110926004423AAR5UZM

Non-Graphical Proof #1

However, I imagine that an analytic proof for the fact that $|\tan x|>|x|$ for these points would be preferred.

By symmetry (i.e. the fact that both tangent and $x$ are odd), it suffices to show this for just $x \in (0, \frac{\pi}{2})$ (in other words, the proof for $x \in (-\frac{\pi}{2},0)$ will be completely analogous up to changes in sign).

This follows from the Taylor expansion of $\tan x$ around $x=0$:

$$\tan x = x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \dots = \displaystyle\sum\limits_{n=0}^{\infty} \frac{U_{2n+1}x^{2n+1}}{(2n+1)!}$$

(See: https://en.wikipedia.org/wiki/Trigonometric_functions#Tangent)

Hence, in particular, it follows that $\tan x > x + \frac{1}{3}x^3 > x$ on the interval in question $x \in (0, \frac{\pi}{2})$.

Completely analogously, $\tan x < x + \frac{1}{3}x^3 < x$ for $x \in (-\frac{\pi}{2},0)$.

Therefore, $|\tan x| > |x|$ for all $x \in (-\frac{\pi}{2},0) \cup (0, \frac{\pi}{2})$, it follows that in particular

$$\frac{\tan x}{x} > 1$$ for all $x \in (-\frac{\pi}{2},0) \cup (0, \frac{\pi}{2})$, and therefore the piecewise defined function in question has a minimum at $x=0$.

For proof without Taylor series:

Note that $x = \int_0^x 1 \text{d}t$ (Fundamental theorem of calculus, the fact that $x'=1$, and $x(0)=0$)

Meanwhile, because $\tan 0 = 0$, as well as the Fundamental Theorem of Calculus, $$\tan x = \int_0^x (\tan t)' \text{d}t = \int_0^x \sec^2 t \text{d}t = \int_0^x \displaystyle\frac{1}{\cos^2 t} \text{d}t$$

Since for $x \in (0, \frac{\pi}{2})$, we have

$$\cos x <1 \implies \cos^2 x < 1 \implies \displaystyle\frac{1}{\cos^2 x} > 1$$

it follows that (since $f>g \implies \int_0^x f \text{d}t > \int_0^x g \text{d}t$):

$$ \int_0^x \displaystyle\frac{1}{\cos^2 t} \text{d}t > \int_0^x 1 \text{d}t$$

which is equivalent to:

$$ \tan x > x,\ \text{for }x \in (0, \frac{\pi}{2})$$.

Using the fact that $\tan(-x)=-\tan x$, it follows immediately that $\tan x < X$ for $x \in (-\frac{\pi}{2},0)$.

Therefore $\left| \displaystyle\frac{\tan x}{x} \right| > 1$ for all $x \in (-\frac{\pi}{2}, 0) \cup (0, \frac{\pi}{2})$, as claimed.

Another One:

By definition of $\cos x$, we have that $$\text{for }x \in (0, \frac{\pi}{2}), 1 < \cos x.$$

Now we show, using this fact, that $$\sin x < x \quad \forall\ x \in (0, \frac{\pi}{2}).$$

Note that $\frac{d}{dx} x =1$ and $\frac{d}{dx} \sin x = \cos x$.

Therefore,

$$\frac{d}{dx} \sin x < \frac{d}{dx} x\ \ \quad \forall\ x \in (0, \frac{\pi}{2})$$

As a result,

$$\int_0^x \frac{d}{dt}\sin t \text{d}t < \int_0^x \frac{d}{dt} t \text{d}t \quad \forall \ x \in (0, \frac{\pi}{2})$$

Because $\frac{d}{dx} x =1$ and $\frac{d}{dx} \sin x = \cos x$, it follows from the fundamental theorem of calculus (sorry but you're going to have learn it eventually and it's not difficult) that

$$\sin x = \int_0^x \frac{d}{dt}\sin t \text{d}t = \int_0^x \cos t \ \text{d}t$$ and $$x= \int_0^x \frac{d}{dt} t\ \text{d}t= \int_0^x 1\ \text{d}t.$$

Therefore it finally follows that

$$\sin x < x \quad \forall\ x\in (0,\frac{\pi}{2})$$.

From this follows immediately that

$$\displaystyle\frac{\sin x}{x} < 1.$$

Now, to show that $$\frac{\sin x}{x} < \displaystyle\frac{\tan}{x}$$

we use the facts that:

$$\tan x := \displaystyle\frac{\sin x}{\cos x}$$

and

$$\cos x < 1 \quad \forall\ x\in (0,\frac{\pi}{2})$$

Hence we get:

$$\displaystyle\frac{\tan x}{x} = \displaystyle\frac{\sin x}{\cos x \cdot x} = \displaystyle\frac{\sin x}{x} \cdot \displaystyle\frac{1}{\cos x} > \displaystyle\frac{\sin x}{x}$$

Then just use any of the arguments in the other answers which rely on these facts being true.

In any case, if you want an answer that's better than "look at this graph, see it's true" (which I already gave by the way), you'll have to use integration and differentiation together (to the best of my knowledge) i.e. the fundamental theorem of calculus.

Answer 4

The function is not bounded. It does not have a maxima or a minima. As $x\to\frac{\pi}{2}^-$, $F(x)\to\infty$ and as $x\to\frac{\pi}{2}^+$, $F(x)\to-\infty$.

---

We already know that for positive $x\in (0, \frac{\pi}{2})$, $$\sin x < x < \tan x$$ Since $x\not=0$, we can divide by $x$ $$\frac{\sin x}{x} < 1 < \frac{\tan x}{x}$$ Hence, $\frac{\tan x}{x}$ is always greater than $1$ for positive $x$. Hence, $f(x)>1$ for all positive $x$.

Moreover, $$f(x) =\frac{\tan x}{x} = \frac{\tan (-x)}{(-x)} = f(-x)$$

Hence, for negative $x$ also, $f(x)>1$

Thus for both positive and negative $x$, $f(x)>1$. On the other hand, at $x=0$, your function is defined to be $1$.

Hence, the minimum occurs at $x=0$ and the minimum value is $1$.