Closed form for non-linear recurrence $a_n=\sqrt{a_{n-1}+6}$ with $a_1=6$

Question

Does equation $a_n=\sqrt{a_{n-1}+6}$ with $a_1=6$ have a closed form? I've found no linearization method. Any suggestion or hint will be highly appreciated.

Answer 1

There is no hope to find an explicit formula for $a_n$, but the asymptotics is clear.

One has $a_n=u(a_{n-1})$ where the function $u:x\mapsto\sqrt{x+6}$ has a unique fixed point $a=3$, hence $a_n-a=u(a_{n-1})-a=u(a_{n-1})-u(a)$ and one can suspect that $a_n\to a$. As a matter of fact, $u(a_n)-a=b_n\,(a_{n-1}-a)$ with $b_n=1/(u(a_{n-1})+a)$ hence $0\lt b_n\lt1/a$ hence $|a_n-a|\leqslant a^{-n}\,|a_0-a|$. Since $a\gt1$, this shows that $a_n\to a$.

More is true: since $b_n\to b=1/(2a)=1/6$, $a_n-a=b^{n+o(n)}$. In other words, since $a_n\gt a$ for every $n$, $$ \lim\limits_{n\to\infty}\frac{\log(a_n-a)}n=\log(b)=-\log(6), $$ and a little more work shows that $a_n-a=c\,b^n\,(1+o(1))$, where $c$ depends on $a_0$ and has no simple explicit form.

Edit: The algebraic trick used above to compute $b$ might hide the fact that $b=u'(a)$, where $a=u(a)$ is the fixed point of $u$.

Answer 2

Rewrite it as $$ a_n^2=a_{n-1}+6\\ a_{n}-a_{n-1}=a_n-a_n^2+6 $$ and approximate it as $$ a_n'-a_n+a_n^2-6=0, $$ which is solved by

$$a_n = \frac{3 e^{5 n}+2 e^{5 c_1}}{e^{5 n}-e^{5 c_1}},$$ with $c_1= \frac15 \left(5-3 \log(2)+\log(3)\right)\;\;$ such that $a_1=6$. Here's a plot...

Answer 3

I think I found closed-form solution for this equation.

We need to find solution for this one ($a_0$ as a first element): $$ a_n = \sqrt{a_{n-1}+6}, \quad a_0=6. $$ We convert equation to this: $$ a_{n-1} = a_n^2 - 6, \quad a_0=6. $$ I always can change direction of element index and rewrite last equation in the next form (we call that equation "eq1"): $$ F_{n+1} = F_n^2 - 6, \quad F_0=6. $$

If we find solution (as function $F(n)$) for that equation we can use it to express the closed-form solution for your problem. If $F_n = F(n)$ then $a_n = F(-n)$. How can we found $F(n)$?

Solution for equation $b_{n+1} = b_n^2, \ \ b_0=\beta$ is $b_n = \beta^{2^n}$. We will seek the solution of the eq1 in this form: $$ F_n = F(n) = f(X^{2^n}) $$ where $f(x)$ is some unknown function and $X$ is some number.

For $f$ we know that $$ f(x^2) = f^2(x) - 6, $$ because we must satisfy the eq1 $$ F_{n+1} = f(X^{2^{n+1}}) = f((X^{2^n})^2) = f(X^{2^n})^2 - 6 = F_n^2 - 6. $$

We use this property and we find $f(x)$ as a fixed point (without proof of existence) $$ f(x) = \sqrt{6 + f(x^2)} $$ $$ f(x) = \lim\limits_{k -> \infty} \sqrt{6 + ... \sqrt{6 + f_0(x^{2^k})}}, $$ (number $6$ in this expression used $k$ times)
where $f_0(x)$ is some random function ($f_0(x) = x$ for example).

Function $f(x)$ are very interesting (it's not elementary or analytic). Here is some of its properties:

1. $f(x^2) = f^2(x) - 6$.

2. $f(0) = f(1) = 3$. $f(x^2) = f^2(x) - 6$ => $f(0) = f^2(0) - 6$ => $f(0) = \frac{1}{2}(1 + \sqrt{1 + 4 \cdot 6})$ => $f(0) = 3.$
   (another proof is to using the formula $\sqrt{c+\sqrt{c+...}} = \frac{1}{2}(1 + \sqrt{1 + 4 c})$.. you can find this on http://en.wikipedia.org/wiki/Nested_radical )

3. $f(a) = 3$ for all $a : |a|<1$. (it's very easy to prove)

4. $f(-x) = f(x)$.

5. $f(x)$ is continuous in all real $x$. (without proof)

Here is a plot of this function:

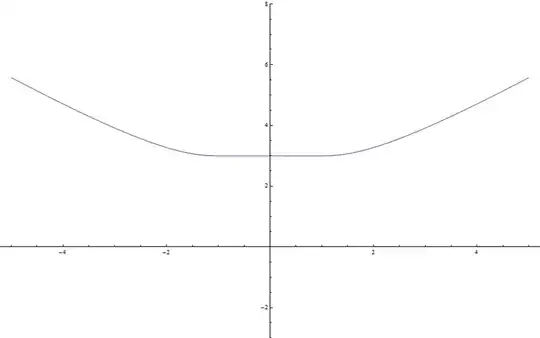
Now we can write the solution of eq1: $$ F_n = F(n) = f(X^{2^n}) $$ where $X$ is positive solution of equation $f(X) = 6$ (because we need satisfy initials $F_0 = f(X) = 6$). ($x \approx 5.46806882358680646837316643$)

Finally we can write the solution for you equation $$ a_n = F(-n). $$

($a_n -> 3$ because $F(-n) = f(X^{2^{-n}}) -> f(1) = 3$)

Same method we can use to find closed-form solution in more general cases!

---

If you have Mathematica you can use my code for check solution:

c = 6; (*constant adder in square root*)
b = 6; (*initial value (for F_0)*)
f0[x_] := x;

(*finding f(x)*)
N1 = 10; (*precision*)
g[x_] := Sqrt[c + x];
f[x_] := Nest[g, f0[x^2^N1], N1];

(*findinf X*)
N2 = 10; (*precision*)
res1 = FindRoot[f[x] == b, {x, c}, WorkingPrecision -> 1000];
X = x /. res1;

F[n_] := f[X^2^n]

(* you can use this function for comparing (this for eq1) *)
F2[n_] := F2[n - 1]^2 - c;
F2[0] := b;

For example:

F[0]
F[-1]
F[-2]

gets

6.00000000000000000000000000000000000000000000000000000000000000000000...
3.46410161513775458705489268301174473388561050762076125611161395890386...
3.07637800264170309696602586393672241931859085772505962544063421316756...

Answer 4

Zegalur: I followed your interesting post but cannot see the final closed form. My first question is why to "change direction of element index" when the changed recurrence Fn+1=F2n−6 is as hard as the original a2n=an−1+6? Has this backward recurrence, say, something to do with symmmetries in a further elaboration? Would you please clarify a bit?

Strange. I can't write any comments.. so I wrote a new answer.. Anyway...

I take a square of two parts of equation and move $6$ to the left side of equation.
$$ a_n = \sqrt{a_{n-1}+6} \ \ \ => \ \ \ a^2_n - 6 = a_{n-1} \ \ \ => \ \ \ a_{n-1}=a^2_{n} - 6. $$ If we have $a_0$ we now can find $a_{-1}, a_{-2}, ...$ ($a_{-1}=30$).

I've changed direction of index because it's more native to work with something like this: $$ F_n = Q(F_{n-1}). $$ (when the next element of sequence is expressed through previous one).

Now $F_{n} = a_{-n}$. If I will find solution in a closed-form $F_{n} = W(n)$ then I can use it to express solution for $a_n$. $$ a_n = F_{-n} = W(-n). $$

It is exactly what I did.

---

You also write that you can't find a final result. That is because solution is expressed by non elementary function $f(x)$ (see my answer). But you can't even find a Taylor series for it. But that function exist and it is continuous (see for example the plot of it).

Final result is $$ a_n = F_{-n} = f(X^{2^{-n}}) $$ where $f$ and $X$ are defined in my previous answer.