How to solve this integral equation with the Dirichlet kernel?

Question

It is

$$ S (t) = 1 - i g \int_0^t d \tau \left( \sum_{n=-M}^M e^{-i n (t- \tau )} \right) S(\tau) . $$

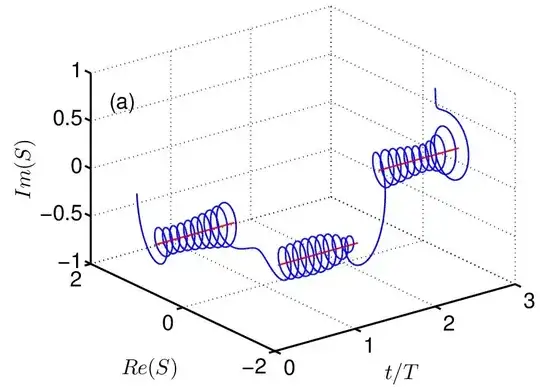
The kernel is the Dirichlet kernel. Numerical result is shown in the figure.

The $M\rightarrow \infty $ limit is easy (because the kernel reduces to a series of delta functions). In this limit, $S$ is a piece-wise constant function, illustrated by the red lines. But for a finite $M$, you will always get the fast rotation whose amplitude does not decay to zero in the limit of $M \rightarrow \infty $. Its amplitude converges to a finite value actually.

The purpose is not to get the analytical expression of $S $ (it might does not exist), but to understand qualitatively its behavior.

It cannot be an arbitrary constant. What were you given here? — Mark Viola, May 08 '16 at 03:47

score 2 · Answer 1 · answered May 08 '16 at 04:24

Nice solenoids...:)

What follows is not a full answer, but hopefully may help

1) Have you tried to take the Fourier Transform of LHS and RHS (the RHS is clearly a convolution) ?
2) As the Dirichlet kernel is a way to work on partial sums of Fourier series, when you say "converges to a finite value", I am almost sure that it has something to do with the Gibbs' phenomenon and its quantization (overshoot by $\approx 0.09 \%$) (https://en.wikipedia.org/wiki/Gibbs_phenomenon)
3) Besides, have a look at "The good, the bad and the ugly of kernels: why the Dirichlet kernel is not a good kernel"(https://www.google.fr/search?q=good+ugly+kernels+Dirichlet&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&ei=n74uV-TpDKus8weJgoS4DQ)

I wondered if the particular results you find are not because, using $\int_0^t \cdots$, you implicitely work with "causal" functions, and in particular with $U(t)D_M(t)$ ($U(t)$ = Heaviside, $D_M$ = Dirichlet) instead of $D_M(t)$. — Jean Marie, May 08 '16 at 04:34

score 2 · Answer 2 · edited Apr 13 '17 at 12:20

The kernel can be written

$$\sum_{n=-M}^M e^{in(t-\tau)}=\frac{\sin\left((M+1/2)(t-\tau)\right)}{\sin\left(\frac12(t-\tau)\right)}$$

The kernel has zeroes when $t-\tau=\frac{2\ell \pi}{2M+1}$, $\ell \in \mathbb{Z}$, $\ell \ne (2M+1)m$, for $m\in \mathbb{Z}$. When $t-\tau\to 2m\pi$, we have

$$\lim_{t-\tau\to 2m\pi }\left(\frac{\sin\left((M+1/2)(t-\tau)\right)}{\sin\left(\frac12(t-\tau)\right)}\right)=2M+1$$

for $m\in \mathbb{Z}$.

Next, note that the limit, $\lim_{M\to \infty}\left(\frac{\sin\left((M+1/2)(t-\tau)\right)}{\sin\left(\frac12(t-\tau)\right)}\right)$, does not exist. However, we can evaluate

$$\lim_{M\to \infty} \int_0^t \sum_{n=-M}^M e^{in(t-\tau)}\,S(\tau)\,d\tau$$

using the approach I presented in THIS ANSWER. Proceeding analogously, we have for $0\le t<2\pi$

$$\begin{align} \int_0^t \sum_{n=-M}^M e^{in(t-\tau)}\,S(\tau)\,d\tau&=\int_0^t\frac{\sin\left((M+1/2)(t-\tau)\right)}{\sin\left(\frac12(t-\tau)\right)}S(\tau)\,d\tau\\\\ &=2\int_0^{(2M+1)t/2}\frac{\sin(x)}{(2M+1)\sin\left(\frac{x}{2M+1}\right)}S\left(t+\frac{2x}{2M+1}\right)\,dx\\\\ &\to \pi S(t)\,\,\text{as}\,\,M\to \infty \tag 1 \end{align}$$

Note that if $2k\pi <t<2(k+1)\pi$, then $(1)$ becomes

$$\lim_{M\to \infty}\int_0^t \sum_{n=-M}^M e^{in(t-\tau)}\,S(\tau)\,d\tau=\pi\left(\sum_{j=1}^k S(2j\pi)+S(t)\right)$$

Could it be possible to obtain your final result by using the fact that the limit of Dirichlet kernel when $M \rightarrow \infty$ is Dirac comb (See $ http://www.theoretical-physics.net/dev/math/transforms.html) ? — Jean Marie, May 08 '16 at 19:44
@JeanMarie Yes, of course. I wanted to avoid using the Theory of Generalized Functions and stick with classical analysis. ;-)) -Mark — Mark Viola, May 08 '16 at 20:15

How to solve this integral equation with the Dirichlet kernel?

2 Answers2