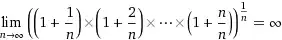Because $(1+\frac{k}{n})\leq (1+\frac{1}{n})^k$ $$ {\sqrt[n]{(1+1/n)(1+2/n)...(1+n/n)}}\leq\sqrt[n]{(1+\frac{1}{n})^{n(n+1)/2}}=(1+\frac{1}{n})^{(n+1)/2}$$ and so $$\lim_{n\to \infty}{\sqrt[n]{(1+1/n)(1+2/n)...(1+n/n)}}<\sqrt{e}$$
But what is the exact limit?
Added: I Gave this to Wolfram and the answer was $\infty$ ! but why?
Take logarithm:
$$\frac1n \sum_{k=1}^n \log \left( 1 + \frac{k}n\right)$$
which converges (using Riemann sums) to:
$$\int_0^1 \log(1+x) dx = 2\log 2 - 1$$
Therefore the original limit is:
$$e^{2 \log 2 -1} = 4/e$$
You can apply Cauchy's limit theorem
$$\lim_{n \to \infty} \sqrt[n]{a_n} = \lim_{n \to \infty} \frac{a_{n+1}}{a_n},$$
with
$$a_n = (1+1/n)(1+2/n)…(1+n/n) = \frac{(2n)!}{n! n^n}.$$
Then
$$\frac{a_{n+1}}{a_n} = \frac{(2n+2)!}{(n+1)!(n+1)^{n+1}}\frac{n!n^n}{(2n)!} \\ = \frac{(2n+2)(2n+1)n^n}{(n+1)(n+1)^{n+1}} \\ = 2\frac{(2 + 1/n)}{(1+1/n)}\frac{1}{(1+1/n)^n},$$
and
$$\lim_{n \to \infty}\sqrt[n]{a_n} = \lim_{n \to \infty}\frac{a_{n+1}}{a_n} = 2 \cdot 2 \cdot \frac{1}{e} = \frac{4}{e}$$
