I know we can present $S_g$ (compact surface of genus $g$) as a $4g$–gon with opposite sides identified, but how to present $S_g$ as a $(4g+2)$–gon with opposite sides identified?
There is an example of $S_2$ (shown in the figure below) on Page 48 of Benson Farb and Dan Margalit's Aprimer on mapping class groups, but I didn't quite understand that.
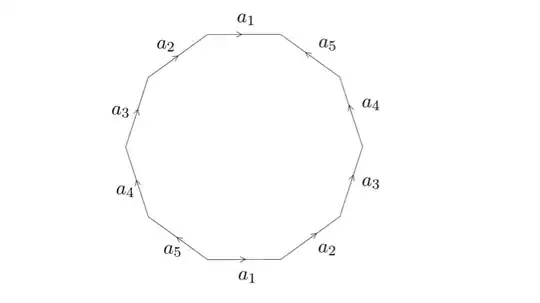
Here's a sketch of a proof that a $4g+2$-gon with opposite sides identified is a surface of genus $g$. The first step is to show it is a surface: Every point has a neighborhood homeomorphic to an open disk. Around interior points of the polygon this is obvious, and around points on the interiors of edges this is also obvious: two half disks glue together to form a full disk. Around vertices, this is less obvious, but what ends up happening is several sectors get glued in such a way as to form a disk.
This surface is orientable since the sides are oriented compatibly (without twists). Finally we calculate the euler characteristic $V-E+F$. There is one face, the interior of the polygon, $2g+1$ edges since the original $4g+2$ are identified in pairs. Finally, in this particular configuration there are only two equivalence classes of vertex. For example, the terminal vertex of $a_1$ at the top is the same as the one at the bottom, which is the same as the initial vertex of $a_2$,and then looking across, the terminal vertex of $a_3$ etc. It is a good exercise to figure out why there are only two equivalence classes in general. So now $V-E+F=2-(2g+1)+1=2-2g$, which matches the Euler characteristic of $S_g$.
Note: Your statement that a genus $g$ surface is obtained from a $4g$-gon with opposite edges identified is not correct. $S_g$ can be obtained by identifying some pairs of edges, but not opposite ones!
