0

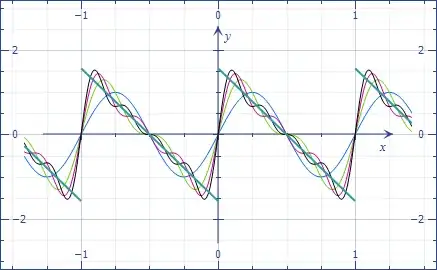
I'm trying to find the value of $\mathbf S$ where

$$\mathbf S = \sum_{k=1}^\infty \frac{\sin(2\pi k x)}{k}; k \in \mathbb N, x \in \mathbb R^*, x \not \in \mathbb N$$

I had a look to WA which lead me to this result.

I think this result can be simplified. So I did some research and some hours later, I found this result:

$$\mathbf S = \pi (x+\frac{1}{2}-(2n+m)) ; n,m \in \mathbb N$$

I'm not satisfied with this result either. I think I miss something on the way.

I'm stuck. What is the result of this infinite sum?

Stephan
  • 188
  • 2
    This is the Fourier series of $f(x) = \frac{\pi}{2} - \pi x$ on $[0,1]$, see e.g. this question. An expression for the sum of the series that holds for all $x\not\in\mathbb{N}$ is $\frac{\pi}{2} - \pi {x}$ where ${x} = x - \lfloor x\rfloor$ is the fractional part of $x$ – Winther May 04 '16 at 00:11
  • It seems that wolfram alpha doesn't understand the Fourier series so well.. I wonder how it could be improved for detecting and simplifying such Fourier series. – reuns May 04 '16 at 00:15
  • 1
    Try writing down the Taylor series of $-\log(1-z)$ at $z=0$, replacing $z$ with $e^{2\pi i x}$ and taking the imaginary part. – Jack D'Aurizio May 04 '16 at 00:39
  • @JackD'Aurizio : but you can't replace $|z| < 1$ by $e^{i t}$ directly, you have to prove also that $\sum_k z^k/k$ converges on $|z|=1, z \ne 1$, and that it is equal to $\lim_{r \to 1^-} \sum_k r^k z^k/k$ – reuns May 04 '16 at 01:01
  • 1
    @user1952009: you are clearly right, one has to be quite careful when acting on the boundary of the pointwise-convergence disk, but Abel's lemma is designed just for that. – Jack D'Aurizio May 04 '16 at 01:05
  • An alternative is to compute $\sum \frac{\sin(2\pi n x)e^{-\lambda n}}{n}$ in a similar way, then apply Dirichlet's test and the dominated convergence theorem in letting $\lambda\to 0$, that is the usual method for computing the continuous analogue $\int_{0}^{+\infty}\frac{\sin x}{x},dx$, too. – Jack D'Aurizio May 04 '16 at 01:10
  • @JackD'Aurizio : if Abel's lemma means summation by part then it is exactly what I wrote on the other post on the functional equation for $\zeta(s)$, so I approve :). – reuns May 04 '16 at 01:15
  • @JackD'Aurizio : but I don't see the dominated convergence as is, I think you'll have to use summation (or integration) by parts too. – reuns May 04 '16 at 01:16
  • @user1952009: oh, sure, we have to apply Abel's lemma (summation by parts) even in that case, I agree. – Jack D'Aurizio May 04 '16 at 01:19
  • Correction: my comment above is slightly misleading. The series is not the standard Fourier series of $\frac{\pi}{2}-\pi x$ but rather what you get by naively adding the Fourier series of $-\pi x$ (the sawtooth) with the Fourier series of $\frac{\pi}{2}[2\theta(x)-1]$ (the square wave) on $(0,1)$. Also: the formua I gave above only holds for $x>0$ for $x<0$ the constant term should be $-\frac{\pi}{2}$. – Winther May 04 '16 at 01:30

1 Answers1

1

Indeed, WA missed some simplification.

$$\log(1-e^{i2\pi x})-\log(1-e^{-i2\pi x})=\log\left(\frac{1-\cos(2\pi x)+i\sin(2\pi x)}{1-\cos(2\pi x)-i\sin(2\pi x)}\right)\\ =\log\left(\frac{2\sin^2(\pi x)-i2\cos(\pi x)\sin(\pi x)}{2\sin^2(\pi x)+i2\cos(\pi x)\sin(\pi x)}\right)=\log\left(-\frac{ie^{i\pi x}}{ie^{-i\pi x}}\right)=i2\pi x+i(2k+1)\pi.$$

So with the factor $\frac i2$ the sum should be

$$\pi\left(k+\frac12\right)-\pi x$$ where $k$ is indeterminate.

As the sine is periodic so is the Fourier series, and the indeterminate $k$ must be some integer offset from the integer part of $x$,

$$\pi\left(\lfloor x\rfloor+n+\frac12\right)-\pi x.$$

Then we can evaluate the series at $x=\frac12$, which is an ordinary point ($x=0$ wouldn't work), get $S(\frac12)=0$, and conclude

$$S(x)=\pi\left(\frac12-\{x\}\right).$$

enter image description here