purplemath.com explains the quadratic formula. I don't understand the third row in the "Derive the Quadratic Formula by solving $ax^2 + bx + c = 0$." section. How does $\dfrac{b}{2a}$ become $\dfrac{b^2}{4a^2}$?
Asked
Active
Viewed 835 times
5
-
It's not becoming, it's identifying the square of the co-efficient of 2x to be added to either side, to make the LHS a perfect square. – lab bhattacharjee Jul 29 '12 at 11:45
-
If you want a very intuitive, easy-to-understand derivation of the quadratic formula, you might want to check out this answer! – Thomas Russell Jul 29 '12 at 11:49
-
@Mouse Hello please tell me is there some wrong procedure in my answer?i am sure you have not downvoted,just because you have asked this question,i need you answer,you opinion – dato datuashvili Jul 29 '12 at 13:33
-
Sorry if I missed any comments, I haven't accessed this site for 2 days haha – Mouse Hello Aug 01 '12 at 08:51
-
@dato Sorry if I missed your answer, I can't seem to find it – Mouse Hello Aug 01 '12 at 08:52
7 Answers
8
$b/2a$ does NOT become $b^2/4a^2$. All that happens in the third row is that $b^2/4a^2$ is added to both sides of the equation.
The bit about taking half of the $x$ term and squaring it is just a means of working out WHAT to add. This is often called "completing the square" - adding a constant term to an expression to turn it into a perfect square, so that one may later take its square root.
7
Remember how to complete the square: $$Ax^2+Bx=A\left(x+\frac{B}{2A}\right)^2-\frac{B^2}{4A^2}$$
So now
$$ax^2+bx+c=0 ---- \text{complete square}$$ $$a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}=-c$$ $$\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$$ $$x_{1,2}+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}$$ $$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
DonAntonio
- 211,718
- 17
- 136
- 287
5
$$ax^2+bx+c=0 - \text{divide by $a$ because $a\neq 0$ }$$ we get $$x^2+\frac{b}{a}x+\frac{c}{a}=0$$ $$x^2+2x\frac{b}{2a}+\frac{c}{a}=0$$ $$x^2+2x\frac{b}{2a}+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}+\frac{c}{a}=0$$ $$x^2+2x\frac{b}{2a}+\frac{b^2}{4a^2}=\frac{b^2}{4a^2}-\frac{c}{a}$$ $$x^2+2x\frac{b}{2a}+\frac{b^2}{4a^2}=\frac{b^2-4ac}{4a^2}$$ $$x^2+2x\frac{b}{2a}+\left(\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$$ if in LHS we use $x=A$ and $\frac{b}{2a}=B$ then we have $$A^2+2AB+B^2=(A+B)^2$$ or $$\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$$ we have two values of square roote $$x_1+\frac{b}{2a}=+\sqrt{\frac{b^2-4ac}{4a^2}}$$and $$x_2+\frac{b}{2a}=-\sqrt{\frac{b^2-4ac}{4a^2}}$$ or $$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
Adi Dani
- 16,949
1
\begin{align*} ax^2+bx+c &= 0 \\ ax^2+bx &= -c \\ x^2+\frac{b}{a}x &= -\frac{c}{a} \\ x^2+2x\Bigl(\frac{b}{2a}\Bigr)+\Bigl(\frac{b}{2a}\Bigr)^2-\Bigl(\frac{b}{2a}\Bigr)^2 &= -\frac{c}{a} \\ \Bigl(x+\frac{b}{2a}\Bigr)^2-\frac{b^2}{4a^2} &= -\frac{c}{a} \\ \Bigl(x+\frac{b}{2a}\Bigr)^2 &= \frac{b^2-4ac}{4a^2} \\ x+\frac{b}{2a} &= \frac{\pm\sqrt{b^2-4ac}}{2a} \\ x &= \frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{align*}
Lok
- 85
0
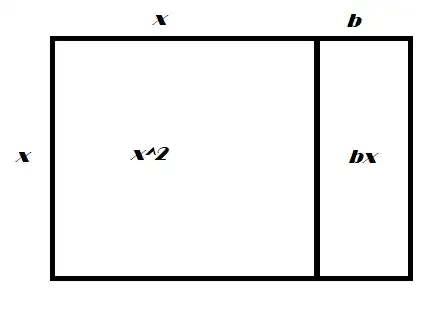
I see no visual proof, so I will add one.
The rectangle below is broken up into to parts: a square and another rectangle. Note that the area of the original rectangle is given by the sum of the two smaller areas: $$x^2 + bx$$
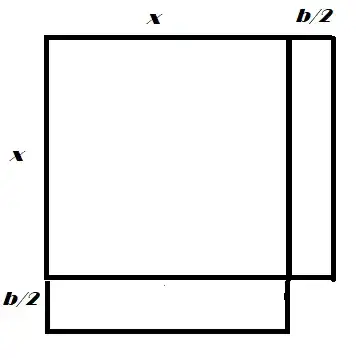
The next step is to divide the smaller vertical rectangle by two, rotate the strip and add it to the bottom:
The new figure is a square with sides $x + \frac{b}{2}$ and a bite out of the bottom right. The bite is also a square, and has sides $\frac{b}{2}$. The area of this figure, then, is the area of the square, less the area of the bite:
$$(x + \frac{b}{2})^2 - (\frac{b}{2})^2$$
But this "square less a bite" figure must have the same area as the original figure, since it was obtained by cutting the original figure and rearranging the pieces. So we can equate the expressions for both these areas:
$$x^2 + bx = (x + \frac{b}{2})^2 - (\frac{b}{2})^2$$
At this point, you can satisfy yourself of the above equality by multiplying out the business on the right, simplifying, and showing that it becomes the expression on the left.
Now you have a way of rewriting quadratics of the form $x^2 + bx$ which will prove to be very useful very soon.
When we're looking for the roots of a quadratic equation, we are looking for the values of $x$ that make it zero. The equation will take on this form: $$Ax^2 + Bx + C=0$$ so let's make it look like $x^2 + bx$. First, divide everything by $a$:
$$x^2 + \frac{B}{A}x + \frac{C}{A} = 0$$
In the previous equations, the coefficent of $x$ was $b$. In this new equation, it's $\frac{B}{A}$. Let's rewrite the above equations, substituting $\frac{B}{A}$ for $b$, and adding in $\frac{C}{A}$ to each side, so it all equals zero:
$$x^2 + \frac{B}{A}x +\frac{C}{A}= (x + \frac{B}{2A})^2 - (\frac{B}{2A})^2 +\frac{C}{A}=0$$
Rearrange a bit and begin to solve for $x$:
$$(x + \frac{B}{2A})^2 = (\frac{B}{2A})^2 -\frac{C}{A}= (\frac{B}{2A})^2 -\frac{4AC}{4A^2}=\frac{B^2-4AC}{4A^2}$$
Take the square root of both sides:
$$x + \frac{B}{2A} =\pm\frac{\sqrt{B^2-4AC}}{2A}$$
And, finally, bring $\frac{B}{2A}$ to the right:
$$x =\frac{-B\pm\sqrt{B^2-4AC}}{2A}$$
MathAdam
- 3,309
0
From Maths is Fun.
Hope this helps