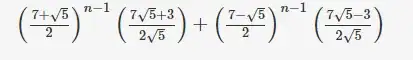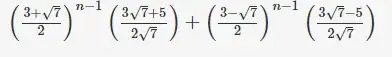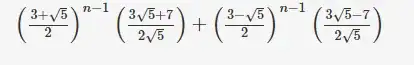0

Let $A$ be an $n × n$ matrix of the following form.

enter image description here

What is the value of the determinant of $A$?

  1. List item
  2. List item
  3. List item
  4. List item

My attempt:

I've used brute force to identity correct option. When I put $n=1$, then determinant of $A$ should be and options give $5, 7, 3, 3$ respectively. Since, options $(3)$ and $(4)$ return same value.

So, I put $n=2$, then determinant of $A$ should be $8$ and option $(3)$ and $(4)$ return $7$ and $8$ respectively. So, option $(4)$ is correct.

Can you explain in formal way? Please.

Mithlesh Upadhyay
  • 4,787

1 Answers1

3

Let $A_n$ be the matrix of the form $$\begin{bmatrix} 3&1&&&&&\\ 1&3&1&&&&\\ &1&3&1&&&\\ &&1&3&&&\\ &&&&\ddots\\ &&&&&3&1\\ &&&&&1&3 \end{bmatrix}_{n\times n}\qquad n\in\mathbb{N}.$$ Then by Solitary' comment, we have $\det A_1=3$, $\det A_2=8$, and for $n\ge 3$, $$\det A_n=3\det A_{n-1}-\det A_{n-2}.$$ Let $a_n=\det A_n$, and define $B=\begin{bmatrix}0&1\\-1&3\end{bmatrix}$ and ${\bf x}_n=\begin{bmatrix}a_{n}\\a_{n+1}\end{bmatrix}$. Then the original pattern of the sequence becomes $$\begin{bmatrix}a_{n+1}\\a_{n+2}\end{bmatrix}= \begin{bmatrix}0&1\\-1&3\end{bmatrix}\begin{bmatrix}a_{n}\\a_{n+1}\end{bmatrix},\quad n\ge 1.$$ That is, \begin{align} {\bf x}_{n+1}= B{\bf x}_n \quad \mbox{for all }n\ge 1,\quad\mbox{with }{\bf x}_1=\begin{bmatrix}3\\8\end{bmatrix}. \end{align} It follows that ${\bf x}_{n+1}=B^n{\bf x}_1$, and we need to find the eigenvalues and eigenvectors of $B$ as below. By a little computation, the eigenvalues are $$\lambda_1=\frac{3+\sqrt{5}}{2}\quad\mbox{and}\quad \lambda_2=\frac{3-\sqrt{5}}{2}.$$ The corresponding eigenvectors are $${\bf v}_1=\begin{bmatrix}1\\ \lambda_1\end{bmatrix}\quad\mbox{and}\quad {\bf v}_2=\begin{bmatrix}1\\ \lambda_2\end{bmatrix}.$$ Let $P=\begin{bmatrix}1&1\\ \lambda_1&\lambda_2\end{bmatrix}$, then $P^{-1}=\frac{-1}{\sqrt{5}} \begin{bmatrix}\lambda_2&-1\\ -\lambda_1&1\end{bmatrix}$ and $$B=P\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}P^{-1}.$$ Therefore \begin{align} {\bf x}_{n+1} &=B^n{\bf x}_1\\ &=P\begin{bmatrix}\lambda_1^n&0\\0&\lambda_2^n\end{bmatrix}P^{-1} \begin{bmatrix}3\\8\end{bmatrix}\\ &=\begin{bmatrix}\ast\\\frac{1}{\sqrt{5}}[\lambda_1^{n+1}(8-3\lambda_2)+\lambda_2^{n+1}(3\lambda_1-8)]\end{bmatrix} \end{align} or \begin{align} \det A &=\det A_n=a_n\\ &=\frac{1}{\sqrt{5}}\left[\lambda_1^{n-1}(8-3\lambda_2) +\lambda_2^{n-1}(3\lambda_1-8)\right]\\ &=\frac{1}{\sqrt{5}}\left[\left(\frac{3+\sqrt{5}}{2}\right)^{n-1}\left( \frac{3\sqrt{5}+7}{2}\right) +\left(\frac{3-\sqrt{5}}{2}\right)^{n-1}\left(\frac{3\sqrt{5}-7}{2}\right)\right]. \end{align} Hence the answer is 4.

Solumilkyu
  • 3,289