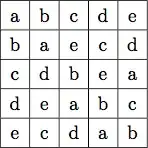
If we fix the first two rows in the above figure, then there are many ways to fill in the remaining rows to obtain a Latin square. Show that none of these Latin squares is the multiplication table of a group.
Hint: Index the first two rows by $x$ and $y$, the first two columns by $u$ and $v$, all under the assumption that we have the multiplication table of a group of order $5$. Show that $(v^{-1}u)^2=1$.
I am not sure how to start this problem. How would we use the hint if we don't know what $u$ and $v$ actually are?