I've tried to detail my question using the image shown in this post.
Consider an ellipse with 5 parameters $(x_C, y_C, a, b, \psi)$ where $(x_C, y_C)$ is the center of the ellipse, $a$ and $b$ are the semi-major and semi-minor radii and $\psi$ is the orientation of the ellipse.
Now consider a point $(x,y)$ on the circumference of the ellipse. The normal at this point on the circumference of the ellipse intersects the major axis at a point $(x_D, y_D)$. This normal makes an angle $/phi$ with the major axis. However, the angle subtended by this point at the center of the ellipse is $\theta$. For a circle, $\theta = \phi$ for all points on its circumference because the normal at the circle is the radial angle subtended by the point on the circumference.
Is there a relationship between the angles $\theta$ and $\phi$ for an ellipse.
For some context, I am trying to "extract" points from the circumference of an ellipse given its parameters $(x_C, y_C, a, b, \psi)$. For such an ellipse, I start from $(x_C, y_C$) and with angle $\theta = 0^\circ$ and I start sweeping until $360^\circ$. Using the equation $\left[\begin{array}{c} x \\ y\end{array}\right] = \left[\begin{array}{c c} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{array}\right] \left[\begin{array}{c} a\cos(\psi) \\ b\sin(\psi) \end{array}\right]$, I get the $(x,y)$ location of the point that is supposed to be on the ellipse circumference. I then look up this location in a list of "edge" points. Along with this list of edge points, I also have gradient angle information for each edge point. This corresponds to the angle $\phi$.
Here is the crux of the question, for a circle, I am confident that the edge point lies on the circumference of the circle if $|\theta - \phi| < \text{threshold}$. But, for an ellipse, how do I get a similar relationship ?
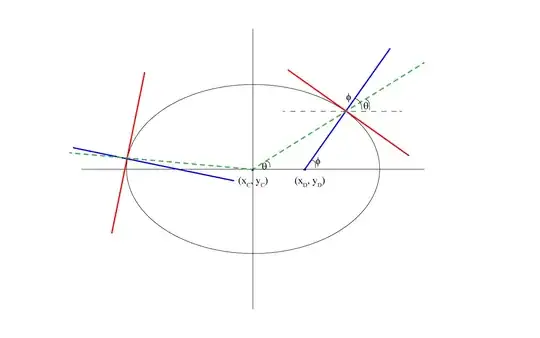
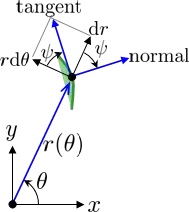
$$\tan\phi = \frac{2v}{b^2}\bigg/\frac{2u}{a^2} = \frac{a^2}{b^2}\frac{v}{u} = \frac{a^2}{b^2}\tan\theta$$
– achille hui Jan 16 '14 at 13:18