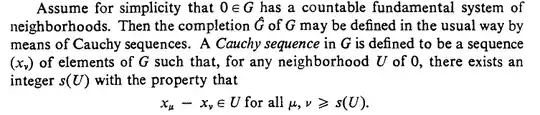Completion $\widehat{G}$ is a topological group

Question

I want to verify that if $G$ is an abelian topological group then so is its completion $\widehat{G}$.

Note that $G$ is not necessarily a metric space. Hence we define a sequence $x_n$ to be Cauchy if for every neighborhood $U$ of $0$ there exists an $N$ such that for $n,m \geq N$, $x_n - x_m \in U$.

It's clear to me that the constant sequence $\bar{0}$ is Cauchy and hence in $\widehat{G}$. It's also clear that if $x_n$ is Cauchy then so is $-x_n$.

The part I'm not sure about is, if we define the group operation elementwise: $\overline{x} + \overline{y} = (x_n) + (y_n) = (x_n + y_n) = \overline{x+y}$, then I need to check two things: first that addition is well-defined, that is if $\overline{x} = \overline{x^\prime}$ and $\overline{y} = \overline{y^\prime}$ then $\overline{x} + \overline{y} = \overline{x^\prime} + \overline{y^\prime}$ and also that $\overline{x} + \overline{y}$ is Cauchy.

So I thought perhaps I could show that $\overline{x} + \overline{y}$ is Cauchy by doing something like this: $x_n + y_n = (x_n - x_m) + (x_m + y_i) + (y_n - y_i)$ but then I cannot say anything about $x_m + y_i$.

Would someone please show me how to verify these two properties? Thank you.

Edit

This is the relevant part in Atiyah-Macdonald:

enter image description here

$x_n + y_n - (x_m + y_m) = (x_n - x_m) + (y_n - y_m)$ and by continuity of addition, given a 0-nhood $U$ there is a 0-nhood $V$ with $V + V \subseteq U$. — martini, Jul 25 '12 at 11:14
Not metrizable? You cannot use mere sequences. Must use something else: nets, filters, neighborhoods, etc. — GEdgar, Jul 25 '12 at 21:34
Sequences should be enough if the topology comes from a subgroup filtration $G_1 \supset G_2\supset \cdots$. Otherwise I have no idea. — Dylan Moreland, Jul 25 '12 at 22:24
@GEdgar Yes, right. We are using a countable neighborhood basis. — Rudy the Reindeer, Jul 26 '12 at 12:17
In a (Hausdorff) topological group: if there is a countable neighborhood basis, then there is a metric for the topology. — GEdgar, Jul 26 '12 at 12:24
There is a metric for the topology of the group, but not for the completion of the group. This will happen if and only if $\cap G_i = {0}$. — the L, Dec 05 '12 at 20:33
One has to verify as well that the sum on $\hat{G}$ is continuous. This is proven here. — Elías Guisado Villalgordo, Sep 08 '23 at 17:08

score 1 · Answer 1 · answered Jul 25 '12 at 21:18

1

In general, if $H$ is a topological group and $G$ is an abelian dense subgroup of $H$, then $H$ is abelian. It follows from the continuity of the sum.

answered Jul 25 '12 at 21:18

Ivan

11

2

Well, first you have to define the sum on the completion. Then show it is a group. Then show it is a topological group. After that, "abelian" follows from the continuity of the sum. – GEdgar Jul 25 '12 at 21:36

Completion $\widehat{G}$ is a topological group

1 Answers1