22

My understanding is that $\cos$ is defined by the value of $x$ as you trace the graph of a circle counterclockwise, starting at the point $(1, 0)$. Similarly, $\sin$ traces the $y$ value. I understand HOW the trigonometric functions work. The issue that has been gnawing at me for years is WHY they are defined that way. There's probably a totally reasonable explanation, I know the history of Trig goes back thousands of years, but I don't understand the reasoning behind defining the Trig functions with the most arbitrary, least intuitive possible rules.

If I had been the person to invent $\cos$ and $\sin$, I would have defined them by starting at the topmost point of a circle, and trace it clockwise. Is that not the most intuitive method? Maybe it's just a modern preference, but it seems to me that we humans like to read things left-to-right, and yet the trig functions are defined starting from a circle's right-most point. Furthermore, $\cos$ and $\sin$ start at $x = 1$ on a circle's graph. Why not start at $x = 0$?

I think this is why so many people have no intuitive understanding of $\sin$ and $\cos$, and why many students get through high school and college by simple rote memorization of what a handful of $x$ values evaluate to in $\sin$ or $\cos$.

user39555
  • 329
  • If you're working in many screen-based 2d graphics libraries, the y axis has positive as down; in these, the trig functions work clockwise. – Dan Uznanski Apr 19 '16 at 07:14
  • For the historical perspective, this is a start: https://en.wikipedia.org/wiki/History_of_trigonometry – Justin Benfield Apr 19 '16 at 07:32
  • 2
    Why did the inventor of the modern analogue clock decide that it should turn in a countertrigwise direction? Especial considering trigonometry was discovered first. – josh Apr 19 '16 at 11:12
  • 9
    @josh clockwise direction was forced by backward compatibility with an already well-known interface, the (Northern hemisphere) sundial –  Apr 19 '16 at 12:39
  • Well that certainly seems reason enough! Very interesting. Rather spoils my humerus and tongue in cheek reference to the semantics raised by the OP in their question. – josh Apr 19 '16 at 13:46
  • What do you mean, they aren't defined starting from the top and going clockwise? Take x=sin(theta) and y=cos(theta)... which is perhaps even the most intuitive mapping from sin/cos to x/y (until you learn the convention). – user253751 Apr 19 '16 at 21:05
  • They arent. Its just that your modern authors/teachers are enforcing a right hand rule. – joojaa Apr 20 '16 at 04:12
  • Let me suggest that the first few angles should have positive rises and runs. Furthermore, we like to see angles measured from the horizon (i.e. x-axis), as early astronomers would have done. One can conclude from those assumptions that standard angles should start from the positive x-axis and proceed in a counter-clockwise direction. – John Joy Apr 20 '16 at 12:51

9 Answers9

19

It's because clockwise angles are taken to be negative while counterclockwise angles are positive. Thus to define the functions, we work on positive angles, hence counterclockwise.

You may ask, why are counterclockwise angles positive and not the other way round?

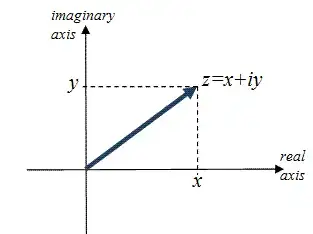
The answer lies in our choice of complex plane.

complex-plane

Our choice while defining complex plane was-

  1. We picked x-axis to be real and y-axis to be imaginary
  2. We chose Positive real part in the right half, positive imaginary part in the upper half

As a result, multiplication by $e^{i\theta}$ rotates the complex plane by the angle $\theta$ counterclockwise.

So, to avoid negative signs in our problems, we say that multiplication by $e^{i\theta}$ rotates the plane by angle $\theta$, not $-\theta$, in other words, we adopt the counterclockwise direction as positive.

Aniket Bhattacharyea
  • 991
  • 26
    Doesn't trig predate complex numbers by more than a millenium? – Barry Apr 19 '16 at 19:09
  • as far as I know, trig function were first defined with arbitrary angles. But when the idea of complex plane was generated, we needed to define positive and negative angles, – Aniket Bhattacharyea Apr 20 '16 at 06:40
  • Not sure I understand your reasoning. If we start at point (0, 1) and move clockwise, 30 degrees clockwise would be the equivalent of 60 degrees counterclockwise starting at point (1, 0), and nothing would be negative and it would be all the more similar to the movements of a clock starting at midday. – Neil Apr 20 '16 at 09:32
  • @Neil That is again just one convention, a direction from the positive X-axis to the positive Y-axis is positive. Of course, some other people can define clockwise as positive. Then everything will change in their co-ordinate system. – Aniket Bhattacharyea Apr 20 '16 at 10:56
  • 1
    @AniketBhattacharyea Of course if it changed now it would create quite the mess, but I'm not proposing to change it. I just don't see the reasoning behind the system that was adopted. It doesn't strike me as more intuitive. – Neil Apr 20 '16 at 12:43
10

I have no insight on historical issues, but my understanding is: precisely because we read left-to-right.

This is how the abscissa axis was born, horizontal and left-to-right. Then the ordinate axis had to be vertical, positive from the ground up to the sky.

As the X axis has precedence over Y (it was born first), nothing is more natural than counting positive angles from positive X to positive Y.

enter image description here

  • 7
    What does counter-clockwise have to do with reading from left-to-right? – Moya Apr 19 '16 at 15:47
  • 4
    Wouldn't the logical conclusion be, that the y-axis points down, since we read from top to bottom (Which is the case for image coordinates in programming most of the time BTW)? – fabian Apr 19 '16 at 17:54
  • @cattywampus: that's precisely what my answer answers. Did you really read it ? –  Apr 20 '16 at 06:55
  • @fabian: that's right. As regards myself, even after practicing image processing for decades (they are using top-down axis), I am still unable to reflect correctly that way. –  Apr 20 '16 at 06:57
  • 1
    @YvesDaoust: Your answer, to me, explains that positive angles are generated counter-clockwise because we move from positive x-axis to positive y-axis. However, I don't see any connection with how reading from left-to-right makes counter-clockwise positive angles natural. As far as what I understand of your answer, you could delete all text except "Nothing is more natural than counting positive angles from positive X to positive Y" and including the diagram. – Moya Apr 20 '16 at 21:47
  • 1
    Also, not all cultures read left-to-right. – Moya Apr 20 '16 at 21:49
  • @cattywampus: https://www.quora.com/In-right-to-left-languages-are-chart-axes-drawn-differently –  Apr 20 '16 at 22:07
5

The reason is presumably because at some point someone decided it made sense to plot trigonometric functions counterclockwise around a unit circle, starting from the $x$ axis, and the convention stuck.

The question then is why that convention made sense. This was probably due to other existing conventions at the time. We have so many other relevant conventions in mathematics nowadays that without looking directly at a lot of very old papers and books I think it would be very hard to say exactly what the influences were.

But it seems highly relevant that trigonometric functions are often defined in terms of triangles, as in this image from https://en.wikipedia.org/wiki/File:TrigonometryTriangle.svg:

enter image description here

The angle whose functions we want to define is angle $A$, an acute angle of a right triangle adjacent to a horizontal leg, which is drawn at the "bottom" of the triangle.

If we want trigonometric functions of angles measured at the origin of an $x,y$ coordinate plane, a natural thing to do is to put this triangle on the plane with vertex $A$ at the origin. Then if we scale the triangle so the hypotenuse is $1$, so that the two legs will simply be the sine and cosine of $A$, we find that the coordinates of $B$ are $(\cos A, \sin A)$; that is, $B$ lies on the unit circle and travels counterclockwise as $A$ increases.

You sometimes see the figure above drawn with vertex $A$ on the right instead of on the left. That would correspond to measuring angles clockwise from the negative $x$-axis. It's not too surprising that that is not the unit-circle convention.

But if this has anything to do with the counterclockwise unit circle, why do we tend to draw the triangle to define functions of the angle $A$ where $A$ is adjacent to a horizontal leg? Why not a vertical leg? I suspect the answer is that we view horizontal lines in a diagram as being parallel to the (local) surface of the Earth, while vertical lines go "straight up", and it is usually easier to measure the angle at which some object appears relative to the ground than relative to the "straight up" direction. Think of a mariner on a ship at sea trying to measure the angle of elevation of the sun or a star with a sextant.

David K
  • 98,388
5

I guess that this relates mainly to the way we identify our coordinate axes. The first axis is the left-to-right $x$ axis. It follows our reading directions, so that consecutive values of a function plot can be read off in reading order. Then we have the $y$ axis perpendicular to that, in such a way that more means up. This is the secondary axis, and order matters here. The first quadrant is the region where both coordinates are positive (or non-negative, if you prefer), and it makes sense to associate that with $[0°,90°]$ as the canonical range of angles for a single quadrant. And in this range, the first endpoint $0°$ is associated with the first axis in $x$ direction, while the second endpoint $90°$ is associated with the second axis in $y$ direction.

There are of course conventions which differ from this. You mentioned the clock, which has $0°$ top and moves clockwise. As Yves Daoust (and a bit later Wumpus Q. Wumbley) pointed out in a comment, the motivation here was likely to mimick sundials, which (on the northern hemisphere) go clockwise as well. A wall-mounted sundial would likely have noon at the bottom, though, so that only explains the choice of zero-point if you consider midnight as the point of reference.

The main benefit in the clock-like scheme is that the special starting direction is vertical, which better fits our day-to-day experience where left and right depend a lot on where we stand, while up is a more universal concept. And this special up direction now serves as an axis of symmetry: changing the sign of the angle exchanges left and right, which is a more common thing than exchanging down and up at least for someone walking on the ground. Apparently reading was more of an influence than walking, though.

There also are areas in computer sciences where $x$ is to the right but $y$ goes downward. This provides a better match for our reading directions, characters in a row from left to right but rows on a page from top to bottom. In such a setup, angles would again be measured clockwise even as the zero direction remains right.

In the end, there is nothing to make one of these convenions more correct than the others, but mathematicians had to settle on one of them to avoid eternal confusion (as still arises with people using one of the other conventions), and at that time apparently reasons for the first choice were prevalent. It might have something to do with our language: if instead of “the value of $f$ at position $x$ is $y$” we were used to saying “we obtain $y$ as the value of $f$ at $x$”, then we might have considered the value axis the first one, and the parameter axis the second, and everything might have worked out differently. (Since most programming languages today use notation like y = f(x), we might be getting there.) Or if the people inventing function plots were more accustomed to reading tabular data from top to bottom, instead of text from left to right, we might have had parameters going that direction. We'll never know.

MvG
  • 42,596
4

Things that are turned: screws, light bulbs, tire lug nuts, spam keys, water faucet handles etc., are usually right-handed. Put your right hand over them and point your thumb in the direction that you want the thing-that-is-turned to move. Your fingers will be pointing in the direction that you need to turn it to make it move in that direction. (Left-handed lug nuts usually have a capital "L" on them to indicate that they are different.)

Three dimensional coordinate systems are usually expected to be right handed. Put your right hand over the origin of the x-y plane and point your thumb in the direction of the positive z-axis. Your fingers will be curled in a counter clockwise direction. That is the direction in which $\theta$ is expected to increase.

Steven Alexis Gregory
  • 26,769
  • 3
    Ancient bicycle shop proverb: Lefty, loosey; righty, tighty. – Senex Ægypti Parvi Apr 19 '16 at 09:40
  • @SenexÆgyptiParvi That saying has always bugged me. Left and right are not directions of rotation. – Reinstate Monica Apr 19 '16 at 18:45
  • @Solomonoff'sSecret The way I make sense of it is, if a screw is pointing away from you, say stuck in a wall, usually it will be near your hands and so below your eye level. Thus the closest point will be the top surface of the screw, which goes left on a counter-clockwise rotation and right for clockwise. Also, if you grab something with your hand (like twisting a cap off), your fingers move left or right while the heel of your hand acts as the pivot. – Mario Carneiro Apr 19 '16 at 22:13
  • 1
    @Solomonoff'sSecret - I think so to. But it doesn't matter as long as it makes sense to the guy with the screwdriver. – Steven Alexis Gregory Apr 19 '16 at 23:03
  • I suspect that should we ever encounter an alien species that this is going to be like observing a child try to fit a triangle prism into a circular hole for them. They'll wonder why we struggle to grasp such a simple concept and why we insist to reduce circular movement to a left or right direction. – Neil Apr 20 '16 at 09:43
  • @Neil If you think of north as "up", all of the planets and almost all of the moons and asteroids in the solar system obey the right-hand rule. I think it would look very reasonable. – Steven Alexis Gregory Apr 20 '16 at 14:15
  • @StevenGregory That's just it, calling the northern artic cap as the "top" of earth is a little silly, though I see where you're getting at. We use it to wrap our heads around it, but I think you assume that aliens would also need to perform tricks like that to understand it. What do you think of people who always have to form L shapes with their hands in order to realize which side is left? Lets just say that probably not the most intelligent people do this. Apply that reasoning to the entire human race. – Neil Apr 21 '16 at 08:39
  • @Neil I have a friend who used to say 'superfluvious' when he meant .superfluous. He did that because, in his mind, that's what he saw when he looked at the word and no one had ever told him he was wrong. People have reasons for the things they do and; even though it may look silly to others, it may even be silly; to them it makes perfect sense. – Steven Alexis Gregory Apr 21 '16 at 18:42
3

The first measures of angles came from the Babylonians - maybe 2500 years ago. They divided circles into 360 degrees, measured the locations of celestial bodies, etc. Trigonometry was developed in the context of spheres and planes at about the same pace, based on the need to navigate long distances.

One important note here: they defined "longitude" to be the degrees around the Earth in a "counter-clockwise" direction. Perhaps because this is the direction of rotation of the Earth ("forward" or toward sunrise on the surface) or the direction of the moon's orbit around the Earth. In either case, this "convention" existed far earlier and with more profound impact to people than any explanation I have seen presented so far. This is the first example of a "right hand coordinate system" I am aware of (if you curl your right hand fingers in the direction of increasing longitude, your thumb points in the direction of "north").

Second, star coordinates are measured based on "elevation" or "altitude" in a horizontal coordinate system - the angle from the horizon. Translating that to writing creates the convention of measuring the angle starting from the x-axis as the horizon. Starting with x=0 and y=1 requires finding the zenith in this system, which is hard to determine using the tools available a long time ago. So it is not a "natural" assumption in that context at all. "Counter-clockwise" is simply the only direction you can go for visible stars in this system.

This provides a basis in nature and history for both the x-axis and the counter-clockwise conventions along with a basis for understanding how a "right hand coordinate system" might even be imagined. I can't say for certain that this is the actual basis for the current convention, but it pre-dates other answers and is the reason trigonometry developed, so I think it provides a better answer to your question.

Jim
  • 211
1

Clockwise or anticlockwise .. is a matter of accepted convention. The results are going to be same, the results depend on constants or invariant relationships. You have to start somewhere and that somewhere is arbitrary. Nothing is sacrosanct, you can have a new law to drive on left, won neve ti egnach nac uoy, but that should not inconvenience the users during changeover. Also after a time people get conditioned to a set of old practices and if you have to change it the cost and time would be viewed as a tremendous wastage serving no purpose. Someone I knew opined the Swastika was unlucky as its design was depicted in a "wrong" direction. Silly.. if you see the sign from the other side is it not then okay? During Hindu temple visits it is considered blasphemous to go around anti-clockwise direction (in plan-view).. if people rotate in both directions they may collide with each other.. or to a show a lamp of worship to God in anticlockwise direction from devotee's side, which the God anyway sees in the clockwise direction. It is old habit becoming custom and sometimes law. Someone initiated it a very long time ago with some logic and it just stuck there by practice ...

Narasimham
  • 40,495
  • The first clock must have been a solar one, hence defining the rotation of time. The trigonometric path must have been later decided by contrariness. –  Apr 19 '16 at 11:45
  • @YvesDaoust Maybe the first clock was on the southern hemisphere? – G. Bach Apr 19 '16 at 12:50
  • 1
    @G.Bach: yep, it was a clepsydra with water flowing bottom up :) –  Apr 19 '16 at 12:58
  • @YvesDaoust I might be slightly too tired, so maybe I made a thinko, but the sun passes from east to north to west in the southern hemisphere, so wouldn't a sun dial go counter-clockwise there? – G. Bach Apr 19 '16 at 13:00
  • @G.Bach: just kidding, don't worry. –  Apr 19 '16 at 13:03
  • There is evidence from a scholar (pre-independence time) BalagangadharTilak reg. Indian ancients of Northern hemisphere ..may have influenced a natural choice of clock movement. https://en.wikipedia.org/wiki/Jantar_Mantar_(Jaipur). – Narasimham Apr 19 '16 at 13:27
1

One of the above answers is correct but the explanation is incomplete. The answer has to do with the right-hand rule. This comes into play when working in three dimensions (calculus 3 especially.) When we use a three dimensional coordinate system, lay your right hand on the x-axis with the fingers pointing in the positive x direction and the palm facing in the positive y direction. If you were to close your fingers toward the y-axis, then your thumb would point in the positive z direction. This is why we set up the 3 dimensional coordinate system in the orientation that we have. Positive x to positive y yields positive z, positive y to positive z yields positive x, positive z to positive x yields positive y. The right hand rule comes into effect in many physics applications, electromagnetism being the foremost one that springs to mind. And thusly, in order to make this a universal standard practice, we start at positive x and move toward positive y when denoting angles, even in two dimensions so that it can translate easily when we add the third dimension, and be in agreement with actual physical properties that can be observed.

Kevin
  • 19
  • 3
    The problem with this is that the right-hand rule in physics was developed much later than the relevant trig convention. (Had we defined things differently earlier, we might just have ended up with a different convention in physics and ended up with a "left-hand rule" instead.) – Silverfish Apr 19 '16 at 20:00
0

The way it was explained to me was as follows. The earth, seen from "the top", i.e. looking down on the north pole, rotates counterclockwise. So do most of the other planets and moons in our solar system. All orbits around the sun are also in that direction. Therefore it was taken as the positive rotation direction. Why (1,0) was used as the starting point is explained in several ways in the other answers.

Olaf Seibert
  • 1