0

After reading some papers, this problem confuses me.

There are different forms of dual problem to the primal problem: $$\underset{x}\min \ \ f(x)$$
where $f(x)$ is a convex function.

  1. By forming the Lagrangian and doing:(S. Boyd convex optimization ch. 6) $$\underset{\lambda\geq 0}\sup \underset{x}\inf \ \ L(x,\lambda)$$

  2. Form the lower linear model: (Y. Nesterov Primal-dual subgradient methods for convex optimization)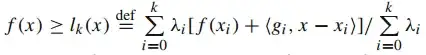

    enter image description here
    The minimization of the right hand side is the lower bound of the primal problem.

And the paper says

dual problem can be posed in different forms depending on the structure of the problem.

My questions is:

How to get intuition or an efficient observation to form a dual problem based on the structure of the primal problem? (In a broad view and sense)

sleeve chen
  • 8,281
  • 1
    This thread might be relevant: http://math.stackexchange.com/questions/223235/please-explain-the-intuition-behind-the-dual-problem-in-optimization – littleO Apr 16 '16 at 06:47
  • @dohmatob You are correct. – sleeve chen Apr 17 '16 at 02:42
  • N.B.: That Nesterov paper is quite dated. What kind of problem are you trying to solve ? – dohmatob Apr 17 '16 at 09:01
  • Actually, I am trying to come up with new idea from these old papers; and one approach is try to adapt the algorithm existing; therefore, I want to build a big picture in this direction. However, I am too junior, so I just ask a suggestion or a possible cut-in point. – sleeve chen Apr 17 '16 at 19:27
  • 2
    The rule should be: if you can algorithmically solve the primal problem directly, do not resort to the dual. If you do, dualise only those constraints which will allow you to solve the dual problem - don't overdualise - unless you gain something, e.g., the dual problem you come up with has a better structure and/or can be solved in a distributed manner. More often than not, there are more than one efficient ways to form a dual problem.

    Additionally, there are more parts of the primal problem than constraints one may dualise and these become more evident in the framework of Fenchel duality.

     – Pantelis Sopasakis Oct 06 '16 at 08:56

0 Answers0