1

Given A = {1,2,3,4}

R4 = {(1,1), (1,2), (2,2), (3,3), (4,4)}.

My understanding is that in the case where if R4 was {(1,1), (2,2), (3,3), (4,4)}, then R4 would be reflexive because every element is reflexive.

In the original problem R4 however, the element (1,2) doesn't show the reflexive property. What makes R4 reflexive given that not all elements of R4 is reflexive??

FocusFort
  • 29
  • 2
  • You are mixing up reflexivity and symmetry. Reflexivity says that $(a,a)$ is in the set for each $a\in A$. It says nothing of $(a,b)$ (where $b\neq a$). – Cameron Williams Apr 14 '16 at 23:39

3 Answers3

2

Since you have asked other questions about relations (with possibly more to come in the future) I think the following explanation should help you a good deal.

It may be helpful to think in terms of (directed multi-) graphs to visualize relations and their properties.

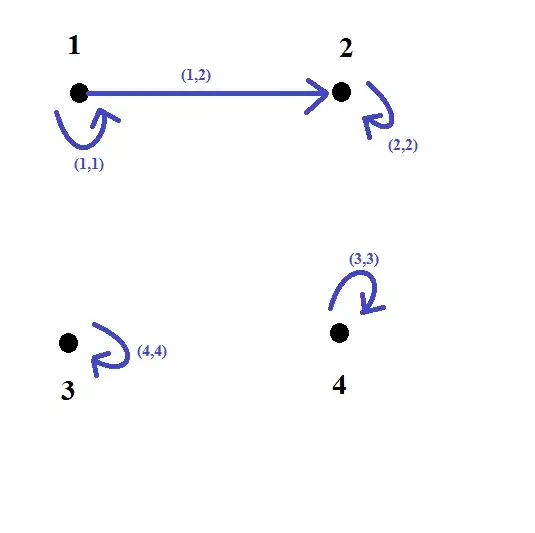
We construct the graph $G$ for the relation $R$ on the set $A$ in the following way:

  • For each element in $A$, draw a vertex and label it.
  • For each pair $(a,b)$ with $a\neq b$ in the relation, draw an arrow starting from vertex $a$ and ending at vertex $b$. $\rightarrow$
  • In the special event that you have both $(a,b)$ and $(b,a)$ are in the relation, instead of drawing a second arrow, make the arrow from $a$ to $b$ doublesided. $\leftrightarrow$
  • For each pair $(a,a)$ in the relation, draw a loop from vertex $a$ ending at vertex $a$.

Your relation:

enter image description here

The usual relation properties we are interested in:

$\begin{array}{|c|l|l|} \hline &\text{Set theoretic}&\text{Graph theoretic}\\ \hline \text{Reflexive}& \forall a\in A, (a,a)\in R&\text{Every vertex has a loop}\\ \hline \text{Symmetric}& \text{If} (a,b)\in R~\text{then}~(b,a)\in R&\text{All arrows (if any exist) are doublesided}\\ \hline \text{Anti-symmetric}&\text{If} (a,b)\in R~\text{and}~(b,a)\in R~\text{then}~a=b& \text{All arrows (if any exist) are singlesided}\\ \hline \text{Transitive}&\text{If} (a,b)\in R~\text{and}~(b,c)\in R~\text{then}~(a,c)\in R& \text{If there exists a directed walk} \\ &&\text{of any length from}~a~\text{to}~b~\text{(a way to travel from}~a~\text{to}~b~\\ &&\text{traveling only in the direction of arrows)}\\ && \text{then there must be an arrow from}~a~\text{to}~b\\ \hline \end{array}$

One can show that each pair of definitions above are equivalent.

In your case, we can see from the graph that it is indeed reflexive since every vertex has a loop, it is not symmetric since there exists an arrow which is not doublesided, it is antisymmetric since there does not exist an arrow that is doublesided, and it is transitive since every directed walk possible in the graph has a directed edge that takes you from start to end in one step.

JMoravitz
  • 79,518
0

Reflexivity of a relation means that all elements of the base set are related to themselves, and not that all related pairs are identical (which would be in one sense a dual property).

For example, the relation $\le$ is reflexive while $<$ is not.

Berci
  • 90,745
0

In the original problem $R_4$ however, the element $(1,2)$ doesn't show the reflexive property. What makes $R_4$ reflexive given that not all elements of $R_4$ is reflexive?

Reflexion is the property of the relation that any element in the underlying set are related to themselves.   Given some relation of a set, $R\subseteq A^2$, when $\forall x\in A: (x,x)\in R$, then and only then is $R$ called a reflexive relation (of $A$).

This does not prohibit the relation from containing other pairs.   It is just a minimum requirement; that at least all of the given type of pairs are in the relation.

In this case, any relation $R$ where $\{(1,1), (2,2), (3,3), (4,4)\} \subseteq R \subseteq A^2$ is a reflexive relation of $A$.

$R_4$ qualifies.

Graham Kemp
  • 129,094