How to generalize the Arithmetic geometric mean

Question

Finding the AGM of two terms is well understood. Since both its Arithmetic and Geometric components can be generalised (identity for a single term, undefined for fewer), can the AGM also be generalised? I would assume yes and further assume identity for a single term undefined for less than one term. I would expect an implementation to use multi term implementation in the first round and the optimised two term variant until it converges (for a given precision).

Answer 1

I am certainly not versed in that matter, but my intuition tells me this: the geometric mean is the antilogaritm of the arithmetic mean of the logarithms. Similarly, the harmonic mean is the inverse of the arithmetic mean of the inverses. More generally, means can be related to the arithmetic mean by $T^{-1}(\overline{T(x)})$, where $T$ is an invertible scalar transform.

For a particular definition of a mean, the transformation can be discovered from a functional equation involving just two values. And as the means are homogeneous functions, one of the values can be $1$ WLOG.

For the geometric mean, the equation reads

$$T^{-1}\left(\frac{T(1)+T(x)}2\right)=\sqrt x$$ or

$$T(1)+T(x)=2T(\sqrt x).$$

And for the AGM, it would be

$$T(1)+T(x)=2T(AGM(1,x)).$$

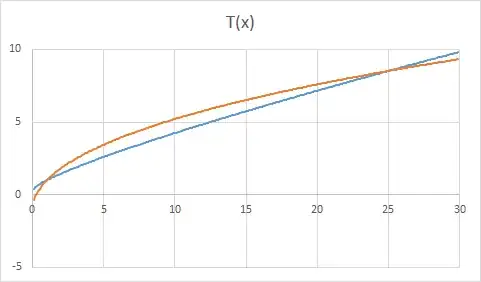
Here is a plot of a numerical estimate, with $T(1)=T'(1)=1$ (orange curve, blue is the $AGM$).

Answer 2

I find the "naive implementation" somehow less than satisfying.

The nice thing about the AGM of two terms is that you start with two terms $a_0$ and $g_0$ and calculate $a_{r+1}=f_1(a_r,g_r)$ and $g_{r+1}=f_2(a_r,g_r)$. There is a mapping from two terms to two terms to two terms to ...

The naive implementation suggests a first stage in which there is a mapping from $n$ terms to 2 terms, after which there is a mapping from 2 terms to 2 terms.

It seems to me that what you really want is $n$ different mappings from $n$ terms to $n$ terms.

So start with $x_{1,0}, x_{2,0}, x_{3,0}, ... , x_{n,0}$

Have a set of functions $f_1, f_2, f_3, ... , f_n$ such that $x_{k,r+1}=f_k(x_{1,r}, x_{2,r}, x_{3,r}, ... , x_{n,r})$

For $n=2$ we have $f_1(x_{1,r}, x_{2,r})=\frac {x_{1,r}+ x_{2,r}}2$ and $f_2(x_{1,r}, x_{2,r})=\sqrt{x_{1,r} \times x_{2,r}}$

The problem comes in deciding what the third, fourth, etc functions should be. They could be other kinds of means.

To satisfy the property of convergence, it would be good if the functions had the same "centring" effect that means do; namely that $\min(a, b, c, d, ...) \le f(a,b,c,d,...)\le \max(a,b,c,d,...)$

Answer 3

Consider the function $f(x)=\ln x$ for $x>0.$ We have $f''(x)=-1/x^2.$ Since $f''<0$ the graph of $f$ is concave: That is, take points $p1,...,p_n$ on the graph of $f$, take $(u,v)$ belonging to the convex hull of $\{p_1,...,p_n\}$ (...the smallest convex set $S$ such that $S\supset \{p_1,...,p_n\}$... ). Then $(u,v)$ is "below the graph", that is, $$v\leq\ln u.$$ Now, with $p_j=(x_j,y_j)=(x_j,\ln x_j)$ for $j=1,...,n,$ the convex hull of $\{p_1,...,p_n\}$ is equal to the set of points of the form $$(\;\sum_{j=1}^n w_jx_j,\;\sum_{j=1}^nw_jy_j\;)$$ for non-negative $w_1,...,w_n$ satisfying $\sum_{j=1}^nw_j=1.$ Therefore for some such $w_1,..,w_n$ we have $$\sum_{j=1}^nw_j\ln x_j=\sum_{j=1}^nw_jv_j=v \leq \ln u=\ln (\sum_{j=1}^nw_jx_j).$$ Since $v\leq \ln u\iff e^v\leq u,$ we have therefore$$\prod_{j=1}^n(x_j)^{w_j}\leq\sum_{j=1}^nw_j x_j$$ whenever each $x_j>0$ and each $w_j\geq 0$ and $\sum_{j=1}^nw_j=1.$ In particular when $w_j=1/n$ for each $j,$ we have $$[\;\prod_{j=1}^n( x_j) \;]^{1/n}=\prod_{j=1}^n (x_j)^{1/n}\leq \sum_{j=1}^nx_j/n=\frac {1}{n}\sum_{j=1}^nx_j.$$ Observe that the graph of $f$ is strictly concave: So if $n>1$ and none of the $w_j$ is $0,$ then none of the inequlities are equalities unless $p_1=p_2=...=p_n,$ that is, unless $x_1=x_2=...=x_n.$

Answer 4

As I said in my first attempt at answering, I find the "naive implementation" somehow less than satisfying because there are different stages.

So I thought again about the mean of three numbers. It can be shown that you don't have to add all three values together and divide by three. Instead you can take this approach:

Start with $a_{1,0}=x_1, a_{2,0}=x_2, a_{3,0}=x_3$

Set $a_{1,1}=\frac {a_{1,0}+a_{2,0}}2, a_{2,1}=\frac {a_{2,0}+a_{3,0}}2, a_{3,1}=\frac {a_{3,0}+a_{1,0}}2$

Repeating this gives values that converge to the arithmetic mean.

You can do something simliar with the geometric mean.

So my suggestion for you is this:

Start with $x_1, x_2, x_3, ... , x_n$

Set $a_{1,1}=\frac {x_1+x_2}2, a_{2,1}=\frac {x_2+x_3}2, ... , a_{n-1,1}=\frac {x_{n-1}+x_n}2, a_{n,1}=\frac {x_{n}+x_1}2$

Set $g_{1,1}=\sqrt{a_{1,1} \times a_{2,1}}, g_{1,2}=\sqrt{a_{2,1} \times a_{3,1}}, g_{n-1,1}=\sqrt{a_{n-1,1} \times a_{n,1}},g_{n,1}=\sqrt{a_{n,1} \times a_{1,1}}$

Continue in this manner and I think you have what you wanted.