$y''-2\sin y'+3y=\cos x$
I'm trying to solve it by power series, but I just can't find the way to get $\sin y'$. Is there any special way to find it?
Asked
Active
Viewed 703 times
2
-
That's nasty. Are you sure this is what it's supposed to be? Either $2y'$ or $2(\sin x)y'$ would make more sense. – joriki Jul 23 '12 at 01:42
-
Yes, it is $-2\sin y'$ – hinafu Jul 23 '12 at 01:46
-
What are your initial conditions? – Mhenni Benghorbal Jul 23 '12 at 04:25
-
You could use Faà di Bruno's formula for your $\sin,y^\prime$, but it can get messy... – J. M. ain't a mathematician Jul 23 '12 at 05:35
-
Force to use power series method seems to be no problem, however you cannot find all the coefficients so that the purpose can only act approximately but not exactly, since the ODE is out of the form $x^2(a_1x^n+a_2)y''+x(b_1x^n+b_2)y'+(c_1x^n+c_2)y=0$ . – doraemonpaul Jul 23 '12 at 23:02
-
Fourier series method also will face the similar situation. – doraemonpaul Jul 23 '12 at 23:14
-
I would consider the given problem as a small perturbation of the linear problem $$ y''-2 y'+3 y=\cos x$$ which can be solved explicitly. A series would have to start with a solution of the linear problem as "approximation of order zero". What are your initial/boundary conditions? – Christian Blatter Jul 28 '12 at 15:49
2 Answers
6
I think you are unlikely to find the power series in closed form, and that even if you did, the next logical step would be to discard all but finitely many terms of the series. So it makes sense to look for a Taylor polynomial of fixed degree from the beginning. For example, if we are okay with 4th order approximation $y=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4 +O(x^5)$, then the linearization $\sin y'=y'+O(x^3)$ is acceptable. It gives the system $$2 a_2 - 2 a_1 + 3 a_0 = 1$$ $$6 a_3 - 4 a_2 + 3 a_1 = 0$$ $$12 a_4 - 6 a_3 + 3 a_2 = -1$$ which is easy to solve especially if given initial conditions for $a_0,a_1$.
If linearization is too crude for your purpose, then consider the approximation $y=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4 +a_5x^5+a_6x^6+O(x^7)$, which requires $\sin y'=y'-(y')^3/6+O(x^5)$ in the equation. The resulting system is nonlinear, but it's just as easy to solve as the previous one, if you begin with known initial conditions $a_0,a_1$. Indeed, the first equation gives $a_2$, the second $a_3$, and so on. Here is how the system looks in Maple:
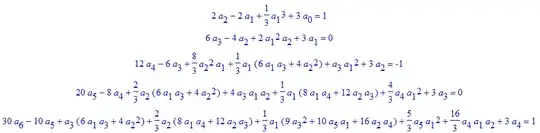
I wonder if there is a name for such systems (it would be triangular if linear).
2
Maple finds the two fundamental solutions:
(with $y(0)=0$ and $y'(0)=b$) $$\eqalign{ y \left( x \right) &=bx+ \left( \sin \left( b \right) +{\frac {1}{2}} \right) {x}^{2}+ \left( \frac23\,\cos \left( b \right) \sin \left( b \right) +\frac13\,\cos \left( b \right) -\frac12\,b \right) {x}^{3}\cr+& \left( \frac2 3\, \left( \cos \left( b \right) \right) ^{2}\sin \left( b \right) - \frac23\,\sin \left( b \right) -{\frac {1}{2}}-\frac14\,\cos \left( b \right) b+\frac12\, \left( \cos \left( b \right) \right) ^{2} \right) {x}^{4}\cr+& \left( \frac45\, \left( \cos \left( b \right) \right) ^{3}\sin \left( b \right) -{\frac {11}{10}}\,\cos \left( b \right) \sin \left( b \right) +{\frac {3}{20}}\,\sin \left( b \right) b-{\frac {13}{15}}\, \cos \left( b \right)\right. \cr& \left.+\frac38\,b-\frac25\, \left( \cos \left( b \right) \right) ^{2}b+\frac45\, \left( \cos \left( b \right) \right) ^{3} \right) {x}^{5}\cr +&O \left( {x}^{6} \right) \cr} $$
and (with $y(0)=a$ and $y'(0)=0$)
$$y \left( x \right) =a+ \left( -\frac32\,a+{\frac {1}{2}} \right) {x}^{2}+ \left( -a+{\frac {1}{3}} \right) {x}^{3}-\frac18\,a{x}^{4}+ \left( \frac14\,a -{\frac {1}{15}}+{\frac {9}{20}}\,{a}^{3}-{\frac {9}{20}}\,{a}^{2} \right) {x}^{5}+O \left( {x}^{6} \right) $$
Arbitrarily many terms of the series can be found (but they get complicated).
Robert Israel
- 448,999