4

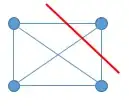
In the Wiki:

https://en.wikipedia.org/wiki/Connectivity_(graph_theory)

It says:

A complete graph with n vertices, denoted $K_n$, has no vertex cuts at all.

Also, the node connectivity of a complete graph ($n$ nodes) is $n-1$

I review the definition of "vertex cut" or "cut" in wiki:
https://en.wikipedia.org/wiki/Cut_(graph_theory)

a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition.

I really have no idea why a complete graph has no vertex cut by the definition? (I can still do the following:

enter image description here

sleeve chen
  • 8,281

3 Answers3

4

I am answering this because I don't have the reputation to comment yet. I was reading through the Wiki article you linked to on Connectivity. The problem is that the term "vertex cut" is defined differently on that article. It is defined as : "A cut, vertex cut, or separating set of a connected graph G is a set of vertices whose removal renders G disconnected." This is indeed the definition of a vertex cut. (https://proofwiki.org/wiki/Definition:Vertex_Cut) If you use this definition, then indeed it is true that $K_n$ has no vertex cut. We can simply remove any set of vertices we want to and then prove that each vertex is still connected to each other vertex and hence the graph is still connected. I think it is just a problem with the definitions that you are facing.

sidhant
  • 300
2

A cut is not the same as a vertex cut. However, it is my opinion that the complete graph $K_n = (V,E)$ has one trivial vertex separator $S$, namely the set $S = V$ consisting of all vertices, since the empty graph should be regarded as disconnected. This convention does not seem to be universally accepted, but similar conventions are customary in other branches of mathematics (the number 1 is not prime, the empty topological space is not connected, the zero ring is not a field, etc.).

Community
  • 1
Josse van Dobben de Bruyn
  • 6,747
  • That is what I was pointing out. The definitions on Wikipedia were misleading. – sidhant Apr 09 '16 at 00:38
  • Oh, yes, there is an incorrect link on the Wikipedia article about connectivity, as you already pointed out. So the content of my answer is merely that you may want to consider the trivial vertex separator $S = V$, although this is not universally accepted. In hindsight I could have sufficed with a comment. :-) – Josse van Dobben de Bruyn Apr 09 '16 at 23:15
0

I think it is fine. Because, vertex cut denotes the vertices and in Complete graph there is no such vertex, by removing that we can make the graph disconnected. In complete graph removing any vertex still leaves the graph complete.

Ali Khan
  • 1