2

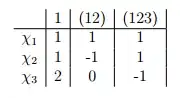
Let $G=S_3$ be the symmetric group on three elements, whose character table is given as follows:

enter image description here

Let $V$ be the unique irreducible representation of dimension $2$

Question 1: Compute the character of the symmetric square representation $Sym^2(V)$

The character of a representation is the trace of a representation. How could one find the trace of $Sym^2V$?

Question 2: Decompose $Sym^2(V)$ into irreducible representations

How do I solve this problem using characters?

I know that the basis elements are:

$e_1^2=e_1 \otimes e_1$, $e_2^2=e_2 \otimes e_2$ and $e_1e_2=e_1 \otimes e_2 + e_2 \otimes e_1$

$\pi \otimes \pi$ acts trivially on $e_1e_2$, and $e_1^2$, $e_2^2$ give rise to $V$

So I believe we have: $Sym^2V \cong 1 \otimes V$

What I would like to know is: how could I have gotten this result by looking at characters

Thanks in advance for your help

Gregory Simon
  • 901
thinker
  • 2,129
  • 1
    for your first question you can see the answer of anon here : http://math.stackexchange.com/questions/137951/symmetric-and-exterior-power-of-representation – Bérénice Apr 04 '16 at 19:49
  • There are many bases for $V$, and to check your computations, we need to know how $G$ acts on the basis that you wrote. So, how does the element $(12)$ act on $e_1$ and on $e_2$? How about $(123)$?

    edit: Or, maybe this is easier: how do you like to think about the representation $V$?

     – Gregory Simon Apr 04 '16 at 23:42

1 Answers1

3

1. The character of $S^2(V)$ can be evaluated using the formula $$ \chi_{S^2(V)}(g)= \frac{\chi_V(g^2)+\chi_V(g)^2}{2} $$ see for example this answer for a proof. Then we have $$ \begin{matrix} & 1 & (12) & (123)\\ \hline \chi_{S^2(V)} & 3 & 1 & 0 \end{matrix}$$

2. If a representation is the direct sum of subrepresentations, then the corresponding character is the sum of the characters of those subrepresentations (wiki).

It should be easy to convince yourself that the only way to obtain $\chi_{S^2(V)}$ as a non-negative integer linear combination of $\{\chi_i\}$ is $\chi_{S^2(V)}=\chi_1+\chi_3$, which proves that

$$ S^2(V)\cong 1 \oplus V $$

In general the decomposition can be found using the fact that the set of irreducible characters is a basis of the vector space of conjugacy class functions. The basis is orthonormal with respect to the scalar product

$$ (\chi_i,\chi_j) = \frac{1}{|G|} \sum_{g\in G} \chi_i(g)\chi_j(g) $$.

In our case $(\chi_{S^2(V)},\chi_1)=1$, $(\chi_{S^2(V)},\chi_2)=0$, $(\chi_{S^2(V)},\chi_3)=1$, giving again the decomposition of $S^2(V)$.

Community
  • 1
fqq
  • 335