0

In the proof of proposition 5.23 Atiyah-Macdonald on page 66 use that if $x$ is algebraic over $K$ and $v = a_n x^n + \dots + a_1 x + a_0$ then $v$ is algebraic over $K$ (where $K$ is the field of fractions of $A$ and $a_i \in A$). I tried to prove it because it seems that it should be easy to prove but didn't manage. Can someone show me how to prove it please?

I posted the statement and the first half of the proof here but my question is about the second part of the proof:

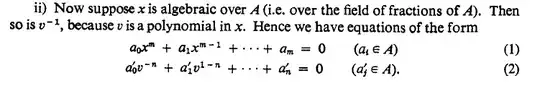
enter image description here

And I have a second question about this proof: in the first half they use the word transcendental to mean transcendental over the ring $A$ whereas in part (ii) of the proof they use algebraic to mean algebraic over the field of fractions. Is the first a mistake? Usually transcendental means transcendental over a field.

Community
  • 1
Rudy the Reindeer
  • 46,359

3 Answers3

4

Regarding your last question:

An element is transcendental over $A$ if and only if it is transcendental over its field of fractions. This because any polynomial over $A$ that is satisfied by $x$ is also a polynomial over $K$, and if you have a polynomial over $K$ satisfied by $x$, then you can multiply by an appropriate constant to clear denominators and get a polynomial over $A$ satisfied by $x$.

All you need to do is show that if $a$ and $b$ are algebraic over $K$, then $a+b$ and $ab$ are algebraic over $K$. The result with then follow from them, since elements of $A$ are certainly algebraic over $K$ (they satisfy the polynomial $t-a$).

To show that this is indeed the case, note that if $b$ is algebraic over $K$ then it is also algebraic over $K[a]$ (same polynomial serves as witness). Therefore, $K[a,b]$ is finite dimensional over $K[a]$, which is finite dimensional over $K$. Thus, $ab,a+b\in K[a,b]$ lie in a finite dimensional vector space over $K$< hence are algebraic over $K$.

Arturo Magidin
  • 398,050
  • I think that sometimes the students are confused by the notions of algebraic number/ algebraic integer, where working over Z or Q is different because we require the polynomials to be monic.. – N. S. Jul 18 '12 at 17:11
  • @N.S. True... which is probably why we often see the terms "algebraic" vs. "integral" to make the distinction. – Arturo Magidin Jul 18 '12 at 17:12
  • Dear Arturo Magidin, thank you very much for this answer! – Rudy the Reindeer Jul 19 '12 at 06:02
2

$x$ is algebric if and only if $K[x]$ is finite dimensional over $K$. Now if $v$ is polynomial in $x$ then $K \subset K[v] \subset K[x]$, thus if $K[x]$ is finite extenioon, so is $K[v]$.

N. S.
  • 132,525
1

If $x$ is algebraic over the field of fractions of the integral domain $A$, there is a nontrivial polynomial $\sum_j \dfrac{a_j}{b_j} x^j = 0$. Multiplying by the product of the $b_j$ we get a nontrivial polynomial with coefficients in $A$. So "algebraic over $A$" and "algebraic over the field of fractions" are equivalent.

Robert Israel
  • 448,999