1

$(\bot E)$ is

$\bot\vdash\psi$.

RAA(Reductio Ad Absurdum) says

If $\{\Gamma,\neg\psi\}\vdash\bot$, then $\{\Gamma\}\vdash\psi$.

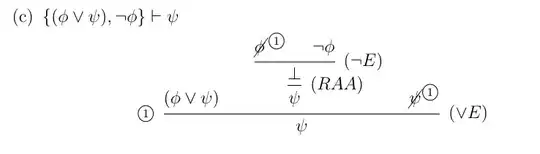
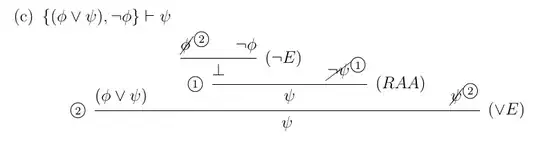
Yet, one of the solutions to my textbook exercises uses $(\bot E)$ and labels it (RAA) in its natural deduction proof as in the picture below. Is it a mistake?

enter image description here

Update 1 : Is the picture below a correct usage of RAA in a natural deduction proof?

enter image description here

  • @MauroALLEGRANZA I added an update to the question. Can you answer my update, too? –  Apr 02 '16 at 09:54

2 Answers2

1

See:

Where the presentation consider both intuitionistic and classical logics, the distinction between:

($\bot$E): $\dfrac \bot \varphi$

and:

(RAA): $\dfrac { [\lnot \varphi] \ldots \bot } \varphi$

has to be maintained.

You can see the answers to what-is-the-correct-reading-of-bot for an overview of the different rules fo the negation.

Community
  • 1
Mauro ALLEGRANZA
  • 94,169
  • I'm using the textbook written by "Chiswell & Hodges". Since the book doesn't explicitly introduce $(\bot E)$ and mention that (RAA) embeds $(\bot E)$, it was difficult to use (RAA) as the authors intended. –  Apr 02 '16 at 09:51
0

About the update, in order to prove the sequent

$\{(\phi \lor \psi),(\neg \phi)\} \vdash \psi$

the following derivation is better:

$ (1)\dfrac{{(\phi \lor \psi)} \quad \quad {\dfrac{ \dfrac{{\not\phi^{(1)}} \quad \quad \quad \quad {\neg \phi}}{\quad \bot}(\neg E) }{\psi}(RAA)} \quad \quad {\not\psi}^{(1)}}{\psi}(\lor E) $

lcmpereira
  • 103