Why this two surfaces have one end?

Question

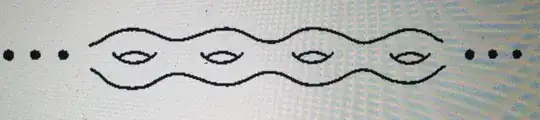
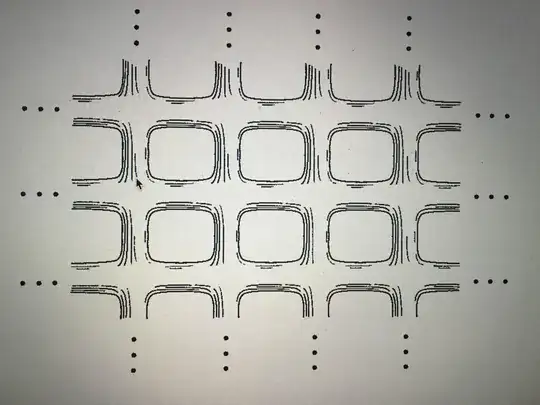
I want to prove that the infinite-holed torus and the infinite-jail cell window have one end but the doubly infinite-holed torus doesn't, my definition of one end is the following:

A locally compact (not compact) space $X$ has one end if for every compact $C \subset X$ there is a compact $K$ such that $C \subset K \subset X$ and $K^{c}$ is connected.

But the thing is that I don't know how to wave my hands here. Can someone help me with this issue?

The pictures:

Thanks a lot in advance.

Not entirely sure what your definition of the infinite-holed torus is, but it sounds as if you're meant to embed $X$ in $\mathbf{R}^{3}$ and let $K$ be the intersection of $X$ with a sufficiently large closed ball. — Andrew D. Hwang, Mar 30 '16 at 01:31

score 2 · Answer 1 · answered Mar 30 '16 at 02:24

2

Follow Andrew's suggestion: First, embed $X$ inside $\mathbb{R}^3$. Then, any compact $C \subset X$ is bounded in $\mathbb{R}^3$, so that you may find a large closed ball $B$ containing $C$. (For the infinite torus you also want to enlarge the ball so that it contains the entire "end" as well as $C$.) Finally take $K = B \cap X \supset C$.

The problem with the doubly infinite torus is that $K^c$ will always be disconnected for any compact $C$ such that $C^c$ is disconnected.

answered Mar 30 '16 at 02:24

Alex Provost

20,991

Is it the same for the jail ? – user162343 Mar 30 '16 at 02:26
1

@user162343 yes, because removing a ball from the jail doesn't disconnect it. – Alex Provost Mar 30 '16 at 02:29
So this is a wave hand proof right ? – user162343 Mar 30 '16 at 02:30
@user162343 It's a bit handwavy yes, but I think it's pretty convincing. – Alex Provost Mar 30 '16 at 02:34
Right :) do you something in algebra ? – user162343 Mar 30 '16 at 02:36
Why we require that $B$ covers the entire "end" if we don't know that is has one? :) – user162343 Mar 31 '16 at 00:41

Why this two surfaces have one end?

1 Answers1

Linked