Perimeter and area of a regular n-gon.

Question

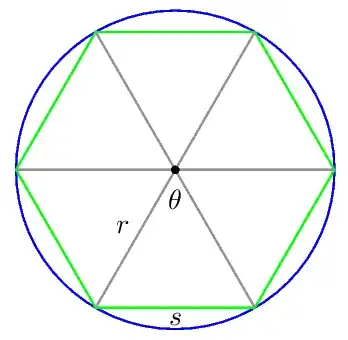
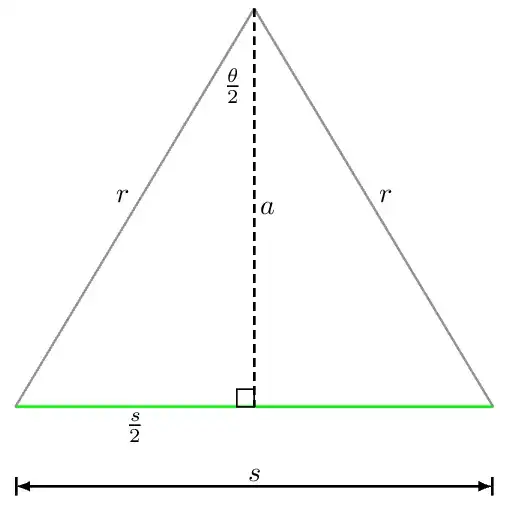
A friend of mine asked me how to derive the area and perimeter of a regular $n$-gon with a radius $r$ for a design project he is working on. I came up with this, but I want to make sure I didn't make any errors before giving it to him.

First, I assumed that the $n$-gon was inscribed in a circle of radius r centered at the origin, with the first vertex of the circle being at the point $(r,0)$.

The vertices of the $n$-gon will divide the circle into $n$ equal sections. Because the total angle of a circle is $2\pi$, then the angle between the $x$-axis and the second vertex is $\frac{2\pi}{n}$. Using trigonometry, the coordinates of this vertex are $\left(r\cos\left(\frac{2\pi}{n}\right), r\sin\left(\frac{2\pi}{n}\right)\right)$.

Now, the origin, the first vertex, and the second vertex form a triangle. The edge of this triangle which touches the circle in two places, using the distance formula, will have a length of $r\sqrt{\left(\cos\left(\frac{2\pi}{n}\right)-1\right)^2 + \left(\sin\left(\frac{2\pi}{n}\right)\right)^2}$.

Now, the $n$-gon will be made up of $n$ of these triangles, and so the perimeter is: $nr\sqrt{\left(\cos\left(\frac{2\pi}{n}\right)-1\right)^2 + \left(\sin\left(\frac{2\pi}{n}\right)\right)^2}$.

Now, the triangle has a base of $r$ and a height of $r\sin(\frac{2\pi}{n})$. There area of a triangle is half the product of its base and height, so the area of the triangle is $\frac{r^2\sin\left(\frac{2\pi}{n}\right)}{2}$.

Again, the $n$-gon is made up of $n$ of these triangles, so its area is: $\frac{nr^2\sin\left(\frac{2\pi}{n}\right)}{2}$

Answer 1

Consider a regular polygon with side length $s$ inscribed in a circle with radius $r$. Let $\theta$ be the measure of a central angle subtended by a side of the regular polygon as shown in the figure below.

As you observed, since a full revolution is $2\pi$ radians, each central angle that subtends a side of an inscribed regular polygon with $n$ sides has measure $$\theta = \frac{2\pi}{n}$$ Each triangle that is formed by connecting the center of the circle to adjacent vertices of the inscribed regular polygon is isosceles since the segments connecting the center to the vertices are radii of the circle.

Let's look more carefully at a triangle formed by connecting the center of the circle to adjacent vertices of the regular polygon. If we draw an altitude from the vertex angle to the base of an isosceles triangle, it bisects both the vertex angle and the base, as shown in the Figure below.

The perimeter of a regular polygon with $n$ sides of side length $s$ is $P = ns$. Since $$\frac{s}{2} = r\sin\left(\frac{\theta}{2}\right)$$ and $$\frac{\theta}{2} = \frac{1}{2} \cdot \frac{2\pi}{n} = \frac{\pi}{n}$$ we have $$\frac{s}{2} = r\sin\left(\frac{\pi}{n}\right) \implies s = 2r\sin\left(\frac{\pi}{n}\right)$$ Hence, the perimeter of the regular polygon is $$P = ns = n\left[2r\sin\left(\frac{\pi}{n}\right)\right] = 2nr\sin\left(\frac{\pi}{n}\right)$$ Note that the length of the altitude of the triangle is $$a = r\cos\left(\frac{\theta}{2}\right) = r\cos\left(\frac{\pi}{n}\right)$$ Hence, the area enclosed by the triangle is \begin{align*} A_{\triangle} & = \frac{1}{2}sa\\ & = \frac{1}{2}\left[2r\sin\left(\frac{\pi}{n}\right)\right]\left[r\cos\left(\frac{\pi}{n}\right)\right]\\ & = \frac{1}{2}r^2\left[2\sin\left(\frac{\pi}{n}\right)\cos\left(\frac{\pi}{n}\right)\right]\\ & = \frac{1}{2}r^2\sin\left(\frac{2\pi}{n}\right) \end{align*} Since the area enclosed by the regular polygon is comprised of $n$ such triangular regions, the area enclosed by the regular polygon is $$A = \frac{1}{2}nr^2\sin\left(\frac{2\pi}{n}\right)$$ which agrees with the answer you obtained by taking one of the legs as the base of the triangle.

Answer 2

The area of triangle $ABC$ can be calculate as $\frac{AB*AC*\sin(B\hat{A}C)}{2}$. Now, divide your n-polygon in n triangles, apply the formula and will obtain the same formula.