8

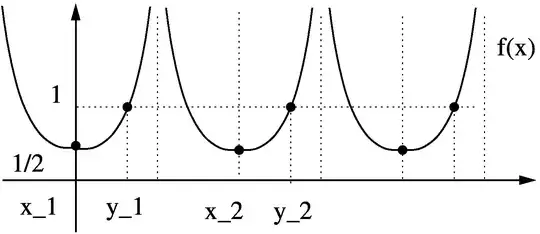
In this question the asker mentions that the limit of this does not exist: $$\lim_{x\to \infty} \frac{1}{1+\cos(x)}$$ Graphically I can see that the limit doesn't exist, but I'd like to know what the proof is. I'm also wondering if there is a general rule that can be applied to any limit to tell if the limit exists.

Sorry if this question is a bit dumb, and thanks in advance for any answers.

Community
  • 1
BombSite_A
  • 83
  • 3
    You could use the fact that the function is periodic and nonconstant. – Travis Willse Mar 24 '16 at 18:24
  • So will any periodic function not have a limit at infinity? – BombSite_A Mar 24 '16 at 18:28
  • Any nonconstant periodic function, as if $\lim_{x \to \infty} f(x) = a$, then $\lim_{k \to \infty} f(a_k) = a$ for any sequence $a_k$ such that $\lim_{k \to \infty} a_k = \infty$. – Travis Willse Mar 24 '16 at 18:30
  • Because there is no interval of type $(a,\infty)$ where the function is defined. For the limit $\lim_{x\to\infty}f(x)$ to exist a precondition is that $f(x)$ must be defined in some interval of type $(a,\infty)$. – Paramanand Singh Mar 25 '16 at 07:09

5 Answers5

16

enter image description here

Let $f$ be a function defined on $\mathbb{R}$ and $\ell\in \mathbb{R}$. Then $\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ if and only if for every sequence $(x_n)$ that tends to $+\infty$, we get $f(x_n) \rightarrow \ell$.

So, in order to prove that a limit $\displaystyle \lim_{x \rightarrow +\infty}f(x)$ does not exist, it is enough to prove that there are sequences $(x_n),~(y_n)$ that tend to $+\infty$ and $\ell_1,~\ell_2\in \mathbb{R}$, such that $\displaystyle \lim_{n \rightarrow +\infty}f(x_n)=\ell_1\neq \ell_2=\displaystyle \lim_{n \rightarrow +\infty}f(y_n).$

In our case: take $x_n=2\pi n,~y_n=2\pi n+\pi/2.$

Nikolaos Skout
  • 5,329
  • 2
  • 16
  • 40
8

As $x$ tends to infinity, there are arbitrarily large $x$ for which $\cos(x) = 1$ and for which $\cos(x) = 0$.

In the former case, the ratio at hand is $1/2$; in the latter case, it is $1$.

If a sequence attains two different values infinitely often, then it cannot converge.

A similar phenomenon is afoot with the limit taken of this expression.

Separately: You probably want your denominator to be slightly different, say, $2 + \cos(x)$.

Right now, you run the risk of encountering $x$ for which $\cos(x) = -1$, which will make the denominator of that expression a rather unwelcome $0$.

Benjamin Dickman
  • 14,451
  • "If a sequence attains two different values infinitely often" - I'm guessing that should be "function" not "sequence", and $f(x) = \frac{sin(\frac 1x)}x$ is a function which attains the values 0 and 1 infinitely often but whose limit is 0 as $x$ goes to infinity. – user253751 Mar 25 '16 at 02:19
  • @immibis No, I quite deliberately wrote sequence rather than function. – Benjamin Dickman Mar 25 '16 at 02:41
6

$\cos(x)$ is periodic. For all values of $x$, $\cos(x)$ will take a value in $[-1,1]$.

It's probably easiest shown by an example. Let's take the cosine of one billion (in radians). $$\cos(10^9) \approx 0.84$$ Then $\frac{1}{1+0.84} \approx 0.54$. Now let's go just a little bit further in $x$, by $\pi/2$: $$\cos(10^9 + \pi/2) \approx -0.54$$

So then $\frac{1}{1-0.54} \approx 2.17$. Do you see why this won't converge? Cosine of $x$ oscillates forever. Consequently, the limit at infinity does not exist.

Newb
  • 17,672
  • 13
  • 67
  • 114
4

Suppose $\lim\limits_{x\to\infty} \dfrac 1 {1+\cos x} = L$.

Then for some number $x_0$, whenever $x>x_0$ then $ \dfrac 1 {1+\cos x}$ is between $L\pm 0.0001$.

There are some values of $x>x_0$ for which $\dfrac 1 {1+\cos x} = \dfrac 1 {1+0} = 1$ and there are some values of $x>x_0$ for which $\dfrac 1 {1+\cos x} = \dfrac 1 {1+1} = \dfrac 1 2$.

Therefore the numbers $1$ and $1/2$ are both between $L\pm0.0001$. That implies $1$ differs from $1/2$ by less than $2\times0.0001$.

Michael Hardy
  • 1
0

If it is Known that any périodic function which admits a limit at + $\infty$ is necessarily constant then the résult follows immediatly because our function is périodic and not constant. The proof of this résult may be conducted by taking two séquences such that f takes a different constant value on each of which. (As Nikolaos skout did)

Idris Addou
  • 4,193