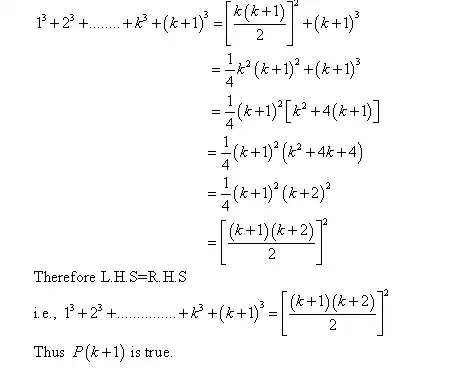0

I'm taking Discrete Structures now and I can't seem to get comfortable with proof by induction. I understand the concept, and the general procedure...but it all just seems like random algebra manipulation and playing around until you get what you want. There are no specific "rules" or guidelines to follow or trends to notice that I am aware of. And if these do exist, please tell me!

For example: Let $P(n)$ be the statement that $$\forall n\in\Bbb{N}:\ 1^3+2^3+···+n^3=\left(\frac{n(n+1)}{2}\right)^{2}$$

Here is the proof for it. How am I supposed to figure out if the algebraic manipulation I'm attempting is even going to lead me in the right direction? Base case and inductive hypothesis:

enter image description here

Proof:

proof

Martin Sleziak
  • 53,687
Laugh7
  • 111
  • where is your initial case and your inductive hypothesis? – Henricus V. Mar 24 '16 at 05:42
  • @HenryW. I added it – Laugh7 Mar 24 '16 at 05:44
  • 3
    Easy Answer: practice, practice, practice. However, in truth, examples of induction are meant to be exercises in algebra. In practice you may see induction when you have a series, such as the solution to a differential equation, and you really want it to have specific behaviour. Induction can help you bridge one to the other, or you notice a pattern and then prove it is true by induction. But the example as you listed above is first and foremost an algebraic exercise. – Mark Mar 24 '16 at 05:56
  • 1
    As you said - it's a lot of algebraic manipulation and as @Mark stated - practice is probably the only way to get more convenient with the concept. I suggest to search here at MSE questions regarding induction and try proving the claims by yourself. Good luck! – Galc127 Mar 24 '16 at 05:58

5 Answers5

1

Remember that it is perfectly fine (although less elegant perhaps) to manipulate both the LHS and the expected RHS to reach an equality. In the proof provided in your question, they use a couple of identities that require some experience to use, and stuff like that might look like "magic" at times.

However, working out the LHS to polynomial form gives.

$$\begin{align} LHS &= \left[\frac{k(k+1)}2\right]^2+(k+1)^3\\ &=\frac14k^2(k+1)^2+(k+1)^3=\\ &=\{\text{...a couple of minutes of work...}\}\\ &=\frac14k^4+\frac32k^3+\frac{13}4 k^2+3k+1 \end{align}$$

And, expanding the expected "RHS" $\left[\frac{(k+1)(k+2)}2\right]^2$ will give you the same result and proof is done.

It's a bit tedious and not as concise, but perfectly fine, and requires less experience.

Daniel R
  • 3,199
1

It is not true that proofs by induction always involve in the inductive step algebraic manipulations. Proofs by induction are used in many areas in mathematics: combinatorics, number theory, graph theory, abstract algebra, linear algebra, ... And inductive step often involves techniques from various areas of mathematics.

On the other hand, it is true that the proofs of statements similar to your example typically involve some algebraic manipulation. (By similar to your example I mean stuff like proofs of various algebraic identities, sums, inequalities, ...)

When proving result about some sum, like in your example, your advantage is that you know in advance what you want to show. In the example with $1^3+2^3+\dots+n^3$ you know that in the inductive step you would like to show the equality $$\left(\frac{n(n+1)}2\right)^2+(n+1)^3=\left(\frac{(n+1)(n+2)}2\right)^2$$ You may notice that both sides have the factor $(n+1)^2$, so this is the same as $$(n+1)^2\left(\frac{n}2\right)^2+(n+1)=(n+1)^2\left(\frac{(n+2)}2\right)^2.$$ Now you see that it suffices to show $$\left(\frac{n}2\right)^2+(n+1)=\left(\frac{(n+2)}2\right)^2,$$ which is a bit simpler.

In general, you know that you want to show that LHS is equal to RHS.

You can try to work a bit on the LHS and to make it more similar to RHS. Then, for a change, you can try to manipulate the RHS for a bit. Eventually you might get to the same expression.

You are probably aware of these posts, but perhaps it is still worth mentioning that you can find posts on this site about the identity you chose as example:

Community
  • 1
Martin Sleziak
  • 53,687
0

That's true, the way to follow for do induction proofs it's about algebraic manipulation. But be careful always you must use induction hypothesis otherwise you can "prove" things that not true, and the Basis step is very important too cause the induction method it's based on well-ordering principle.

The only tips I can do are always write your inductive hypothesis to see what you have for do the proof and write too that you want prove it so in this way you can see the algebraic expresion and try to find a way to factorize the P(k) step from the P(k+1) step and manipulating to get the proof.

Roberto Lopez
  • 11
0

Yes, it is manipulation, but there are conventions and common procedures, especially with sums.

For example if you need to prove: f(1) + f (2) + .... +f (n) = g (n) the induction step will nearly always work like:

f (1)+.... +f (n) + f (n+1) = g (n) + f (n+1)

So nearly always the proof simply involves proving:

g (n)+f (n+1) = g (n+1)

So for example if we need to prove 1+3+5+....+2n-1 = $n^2$, the entire proof boils down to proving:

$n^2 + 2 (n+1) -1 = (n+1)^2$

which is straightforward.

===

Your example $...+n^3 = (\frac {n (n+1)}{2})^2$

is simply a matter of proving:

$(\frac {n(n+1)}{2})^2 + n^3=(\frac {(n+1)(n+2)}{2})^2$.

fleablood
  • 124,253
0

The proof by induction should come to your mind every time you see an expression depending on "n". So always keep it in your mind.

çiçek
  • 83