What is the proof of $$\sum\limits_{k=1}^n(2k-1)=n^2$$ I understand that it derives from $\sum\limits_{k=1}^nk=\frac{n(n+1)}{2}$ but I miss how to relate that proof for this one.
Asked
Active
Viewed 55 times
0
-
First, the top index of your sum ought to be $n$ not $k$. Then just compute $\sum_{k = 1}^n (-1) = -n$ and simplify. – Mar 20 '16 at 19:30
-
Great thanks. I edited the question. – ocram Mar 20 '16 at 19:33
2 Answers
0
You may do this graphically. Consider an $n \times n$ square, divided into smaller unit squares.
The area of this square is, of course, $n^2$.
On the other hand, we can "go up in squares": the first little square in the bottom-left, then the three squares we need to add to get the $2 \times 2$ square in the bottom left, then the five we need to add to get the $3 \times 3$ square in the bottom left, …
Patrick Stevens
- 36,135
0
From the expression $\sum_{k=1}^nk=\frac{n(n+1)}{2}$, you can do \begin{align} \sum_{k=1}^n(2k-1)&=2\left(\sum_{k=1}^nk\right)-\left(\sum_{k=1}^n1\right)\\ &=2\cdot\frac{n(n+1)}{2}-n\\ &=n(n+1)-n\\ &=n^2 \end{align} which proves the statement.
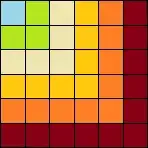
One could also see this intuitively using a picture:
Every color represents a new odd number (there is 1 blue tile, 3 limegreen, 5 white-ish, etc). See how they nicely add up to a square?
Alternatively, we can do it with induction. The base case is obvious, since yes, $1=1^2$. Now assume $\sum_{k=1}^{n}(2k-1)=n^2$ (that's the induction hypothesis). Then: \begin{align} \sum_{k=1}^{n+1}(2k-1)&=2(n+1)-1+\sum_{k=1}^{n}(2k-1)\\ &\stackrel{IH}{=}2(n+1)-1+n^2\\ &=2n+2-1+n^2\\ &=n^2+2n+1\\ &=(n+1)^2 \end{align} Which proves that, if the statement is true for $n$, then also for $n+1$; and since it's true for $n=1$, then also for all $n=1,2,3\cdots$, so for all $n\in\mathbb{N}$.