2

Is there a geometry in which $\pi$, the ratio of a circle's circumference to its diameter, is an integral number such as $3$ or $4$?

Michael Hardy
  • 1
Avi
  • 223
  • 4
    Note that $\pi$ is specifically the name for the ratio between circumference and diamater of a circle in standard Euclidean plane geometry. Even though the ratio between a closed curve of constant diameter to a central point, and twice the radius, may have a different numerical value in other plane geometries, that ratio is then not called $\pi$. – hmakholm left over Monica Mar 16 '16 at 15:14

4 Answers4

13

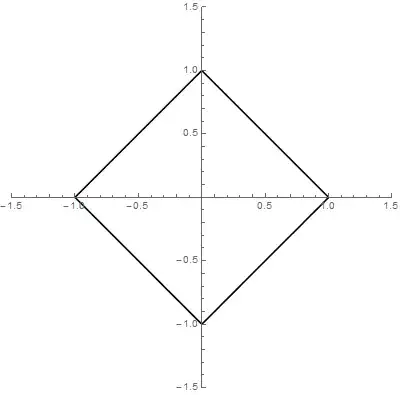
If you use the distance metric of $d=|x_1-x_2|+|y_1-y_2|$ rather than the Pythagorean one then a circle (all points equal distance from a centre) looks like a diamond and the ratio of circumference to diameter is 4.

a circle

Interestingly additional fact if you consider all related distance metrics: $d_n=\left(|x_1-x_2|^n+|y_1-y_2|^n\right)^{\frac1n}$ and draw the corresponding circle and then measure the circumference (non-trivial due to different distance metric) and hence calculate $\pi_n$ that the value we use for $\pi$ (in this case $\pi_2$) is a minimum value for $\pi_n$.

Ian Miller
  • 11,844
4

In spherical geometry, the ratio of a circle's circumference to its diameter is variable. In the concrete case of the equator, circumference/diameter = 2.

Martín-Blas Pérez Pinilla
  • 41,546
  • 4
  • 46
  • 89
1

A cone does the trick nicely, albeit at only one point. Take a sheet of paper and cut a wedge out of it of an angle $\alpha = \pi - 3$ out of it (leaving an angle of 3 radians behind.) Then paste the cut edges together. The set of all points that are a distance $r$ from the cone point has a length of $3r$. In fact, you could do this for any integer $n$; if $n > \pi$, you would need to insert an additional wedge with an angle of $\alpha = n - \pi$ into the cut you make.

Note, however, that $\pi$ is an integer only for circles centered at the cone point. Everywhere else on the surface, $\pi$ is the transcendental number we know and love.

Michael Seifert
  • 9,477
-3

In any geometry, in which circles can be defined, either the ratio of circumference of a circle to its diameter is $\pi$ or that ratio is not a constant. So, no, there is no geometry in which that ratio is constant other than $\pi$.

user247327
  • 18,710