How to compute this integral using residues.

Asked Mar 14 '16 at 14:26

Active Mar 14 '16 at 14:34

Viewed 113 times

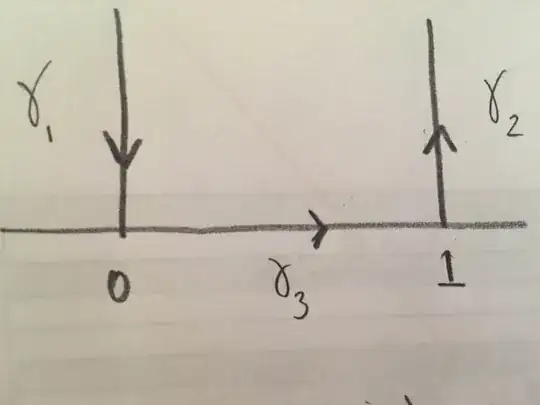
I want to prove that

$$\int_0^1 \log(\sin(\pi x))dx=-\log(2)$$

using the below contour

So,I was trying with $f(z)= \log(\sin(\pi z))$ but I don't know how to compute the residue at $z=0$. The other function I picked was $f(z)=e^{-i \pi z}$ and since it is periodic with period $1$ we have that the integral over $\gamma_1$ and the one over $\gamma_2$ will cancel but the integral over $\gamma_3$ is not the one I want to compute, but in fact I think this didn't work since in this case $f$ is entire.

Another idea I had was to use the definition of the logarithm of a function but I don't know how to extract the desire integral from that information.

Can someone help me with this issue please?

Thanks a lot in advance.

edited Mar 14 '16 at 14:34

gt6989b

54,422

asked Mar 14 '16 at 14:26

user162343

3,245

You can actually compute this integral with just elementary calculus, but I'll see if I can work out a way to do it with residues – ben donahoo Mar 14 '16 at 14:31
Right :) the idea is to use residues :) – user162343 Mar 14 '16 at 14:34
http://math.stackexchange.com/questions/1672030/how-to-calculate-int-0-pi-ln1-sin-x-mathrm-dx/1672067#1672067 u can follow the ideas i used in the link above – tired Mar 14 '16 at 17:11
Ok let me check that out :) just a second – user162343 Mar 14 '16 at 19:39
Well, is not that clear since the integration uses a lot some properties of the given function :( – user162343 Mar 14 '16 at 19:44
what exactly is unclear? – tired Mar 14 '16 at 20:29
Just give me some minutes :) and I'll tell you – user162343 Mar 14 '16 at 21:07
Well the first thing is the change of the contour and obviously you use that in the integral – user162343 Mar 15 '16 at 02:27

How to compute this integral using residues.

0 Answers0